During linear regression, we assume that errors/residuals are normally distributed with mean 0 and some. When we apply the least square method to minimize the error we assume that all the errors have the same variance. This assumption is called homoscedasticity.
More formally homoscedasticity means that,
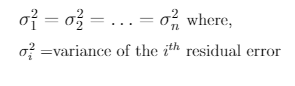
Hence, homoscedasticity in regression is the assumption that all the errors are normally distributed with the same variance. On the other hand, heteroscedasticity means that all the errors do not have the same variance.
Importance of homoscedasticity:
It is very important to detect the presence of homoscedasticity. This is because the conclusions obtained by using the model are valid only under that assumption. If the model is heteroscedastic then the predicted values obtained using the model are not guaranteed to be as close as possible to the actual value of the dependent variable.
How to detect homoscedasticity?
- Homoscedasticity can be detected by constructing a scatter plot of the residuals. If the residuals are scattered randomly then that indicates the presence of homoscedasticity. On the other hand if the residuals are scattered in a non-random manner and trends can be observed then that indicates the presence of heteroscedasticity.
- Bartletts test and Levenes test are some of the tests used to check for the homogeneity of variance. Nowadays, people simply use statistical software to check for homoscedasticity. To know how to check for homoscedasticity in R software click here.
