Bartlett’s test is used to check for the equality of variances of several normal populations. It is most commonly used before applying the ANOVA procedure to test for equality of means. This is because one of the assumptions behind the ANOVA test is the homogeneity of variances.
This means that the ANOVA procedure can be applied only after we have checked that the variances are equal by applying Bartlett’s test.
Procedure to apply Bartlett’s test:
Step 1: Formulate the null and alternative hypothesis as,
H0: The population variances are all equal vs H1: The population variances are not all equal.
Step 2: Calculate the value of Bartlett’s test statistic using the formula,
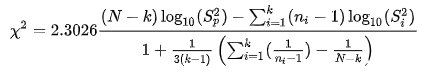
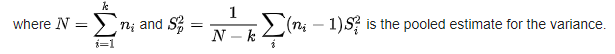
Step 3: The Bartlett’s test statistic follows the Chi-squared distribution with “k-1” degrees of freedom. Calculate the p-value using the test statistic.
Step 4: If the p-value is less than the level of significance we reject the null hypothesis, otherwise we accept the null hypothesis.
Remarks: 1. Bartlett’s test is applicable only under the assumption that the populations are normally distributed.
2. Bartlett’s test can easily be carried out in R software. Click here to know about how to carry out Bartlett’s test in R.
Other tests similar to Bartlett’s test:
- We can apply Levenes test to check for equality of variances if the populations do not follow the normal distribution.
- Box’s M test is applied in the MANOVA procedure to test for the equality of covariance matrices.