The ANOVA (Analysis of Variance) technique is a powerful statistical test that we use to test for equality of means for three or more samples. For example, suppose we want to measure the effect of four kinds of fertilizers on the growth of crops.
Our null hypothesis in the ANOVA procedure will be that the mean growth rate of crops for all four fertilizers is equal. We then apply the F statistic value test to test the null hypothesis.
Some of the different kinds of ANOVA procedures are One Way ANOVA, Two Way ANOVA, and factorial ANOVA. The well-known ANCOVA technique is a generalization of ANOVA.
One Way ANOVA:
We apply the one way ANOVA procedure when there is only one independent variable. So in our example, our independent variable was the type of fertilizer.
The formulae for the one-way ANOVA test are summarised in the below image.
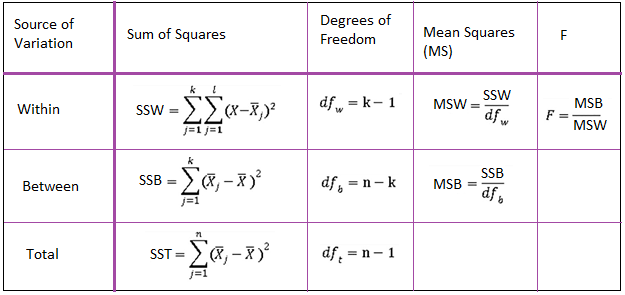
The procedure to apply the one-way ANOVA test is as follows:
- Formulate the null hypothesis that there is no significant difference between sample means.
- Calculate the sum of squares due to treatment and the sum of squares due to error.
- Calculate the mean sum of squares by dividing the sum of squares with the respective degrees of freedom.
- Calculate the value of the F statistic
- If the F statistic exceeds the critical value then null hypothesis is rejected.
- If the F statistic does not exceed the critical value then we conclude that null hypothesis is true.
Two way ANOVA:
We apply the two-way ANOVA procedure when there are two independent variables. For example, we may want to study the effect of the type of fertilizer as well as the quality of soil on the growth rate of crops.
Here one of the two independent variables is called treatments and the other independent variables are called blocks.
The procedure to apply the one way ANOVA test is entirely similar to the two way test except for the fact that we calculate both the mean sum of squares due to treatment as well as the mean sum of squares due to blocks.
Factorial ANOVA:
Factorial ANOVA is applied when there are ‘levels’ or ‘dosages’ of a particular treatment. For example, we might have two different dosage levels for a single fertilizer applied to crops – low or high.
We might also have two kinds of soil – low quality and high quality. Then studying the effect of these treatments at different ‘levels’ on the growth rate of crops requires the usage of the factorial ANOVA technique.
The advantage of the factorial ANOVA technique is that it allows us to study the interaction effects between the treatments and also gives us the maximum efficiency for the estimates of these effects.
Assumptions behind ANOVA:
- The observations are independent.
- The errors are distributed normally.
- The variances of the several normal populations (corresponding to different treatments) are equal. This property is called homoscedasticity.