Levene’s test is used to check for equality of variances of two or more populations where the populations may not follow the normal distribution. Thus the Levenes test is similar to Bartlett’s test but applied in the context of non-normal populations. (The Bartletts test is used when the population follows normal distribution).
It is important to check for equality of variance because it is an important assumption in many statistical procedures such as ANOVA, ANCOVA, etc. The assumption of the equality of variance is also known as homoscedasticity (or homogeneity of variance).
Hypotheses for Levene’s test:
The null hypothesis for the Levenes test is that the variances of all the chosen ‘k’ number of populations are equal.
The alternative hypothesis is that all of the variances are not equal.
Procedure to carry out Levene’s test:
Levene’s test is usually carried out using statistical software such as R, SPSS, etc. This is because the calculations involved in the test are too cumbersome to carry out by hand.
- Click here to understand how to carry out the Levene’s test on R software.
- This video explains how to carry out the Levene’s test on SPSS.
We explain below how to carry out Levene’s test by hand.
The test statistic for Levene’s test:
We first calculate the test statistic for Levene’s test using the formula,
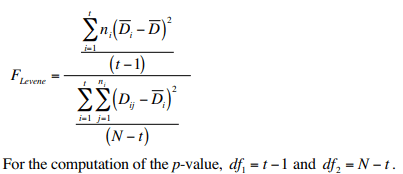

Now you can find the F table value for t-1 and N-t degrees of freedom. If the test statistic exceeds the critical value we reject the null hypothesis, otherwise, we accept the null hypothesis.
Alternatively, you can find the p-value using the test statistic. If the p-value is less than the chosen level of significance then we reject the null hypothesis and conclude that the variances are unequal. If the p-value is more than the level of significance we accept the null hypothesis and conclude that the variances are equal.