The trinomial distribution is a discrete probability distribution used to calculate probabilities in situations where a trial having three possible outcomes is repeated ‘n’ number of times.
It is a generalization of the binomial distribution which is used when a trial has exactly two outcomes.
Example of a situation requiring the use of Trinomial Distribution:
If a toss a coin 10 times then we use the binomial distribution to calculate the probability of getting a certain number of heads. This is because a coin toss has only two outcomes- heads or tails.
Now, suppose a game between 3 players A, B, and C is repeated 10 times. Here we use the trinomial distribution to calculate the associated probabilities since there are three possible outcomes for each game- player A wins, player B wins and player C wins.
How to calculate probabilities using the Trinomial Distribution?
We can calculate the probabilities by substituting the values of the random variables in the joint probability function of the distribution.
Let X denote the number of times the 1st outcome occurs and let p1 denote the probability of the occurrence of the 1st outcome.
Similarly, let Y denote the number of times the 2nd outcome occurs and let p2 denote the probability of the occurrence of the 2nd outcome.
If the total number of trials is ‘n’ then the third outcome clearly occurs “n-x-y” times.
The joint probability mass function of X and Y is given as,
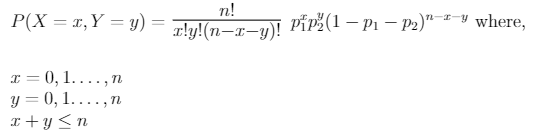
Example:
Suppose a game between 3 players A, B, and C is repeated 12 times. Player A has a 50% chance of winning a game, player B has a 30% chance of winning the game, and Player C has a 20% winning probability.
Calculate the probability that player A wins 4 games, player B wins 3 games and player C wins the remaining 5 games.
Solution: Let X and Y denote the number of games won by players A and B respectively. We are given p1=0.5, p2=0.3, and p3=0.2.
Substituting all this in the above formula we get,
P(X=4, Y=3) = (12! /4!*3!*5! )*(0.5)4*(0.3)3*(0.2)5 = 0.0149688.
Marginal Probability distribution of X and Y:
If we consider X as a random variable in its own right then we see that only two outcomes are possible- either 1st outcome occurs or does not occur. Hence the marginal probability distribution of the random variable X is the binomial distribution with parameters n and p1.
Similarly, the marginal probability distribution of the random variable Y is the binomial distribution with parameters n and p2.
We can calculate the mean and variance of the variables X and Y jointly following the trinomial distribution by using the formula,
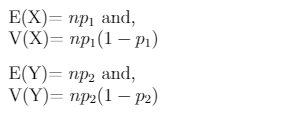
Correlation between X and Y:
It is clear that the two variables X and Y are not independent. Higher values of X imply lower values of Y since we know that the sum X+Y cannot exceed ‘n’. This means that X and Y are correlated (they are covariates).
In fact, we can calculate the correlation coefficient, which measures the linear relationship between X and Y. The correlation coefficient can be calculated using the formula,
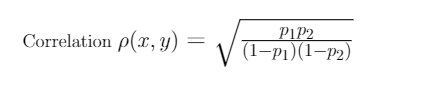
Example:
Given (X, Y) jointly follows the trinomial distribution with parameters n=10, p1=0.2, and p2=0.5. Calculate the mean and variance of X and Y and the correlation coefficient between them.
Solution: We calculate the mean and variance using the above formula,
E(X) = np1= 10*0.2 = 2
V(X) = np1(1-p1)= 10*0.2*0.8 = 1.6
E(Y) = np2= 10*0.5 = 5
E(X) = np2(1-p2)= 10*0.5*0.5 = 2.5
The correlation coefficient is calculated as,
ρ = √(0.2*0.5/0.8*0.5) = √0.25 = 0.5
Trinomial and Multinomial Distribution:
The trinomial distribution is a particular case of the multinomial distribution. The multinomial distribution is used to calculate probabilities when a trial has three or more possible outcomes.
For example, when a dice is thrown there are 6 possible outcomes. We would use the multinomial distribution to calculate probabilities in this case.