The memoryless property is a property of a probability distribution that tells us that the chances of an event occurring now are independent of whether the event has occurred in the past or not. That is why this property is also called the forgetfulness property since the random variable does not “remember” the past and thus the past has no influence on its current behavior.
The more precise mathematical statement of the memoryless property is as follows,
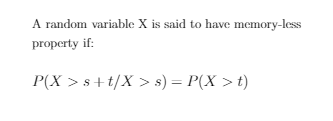
The most well-known distribution that has the memoryless property is the exponential distribution. In fact the exponential distribution is the only continuous distribution that has the memoryless property.
As an example of a memoryless property, suppose that you are waiting in a bank queue with waiting time following exponential distribution. The probability that you have to wait for 2 more minutes is independent of whether you have been waiting for the past hour or not. This, of course, is not very realistic and therefore in real-life queuing models, we frequently use distributions that do not have the memoryless property for modelling purposes.
The geometric distribution is another example of a distribution that has memoryless property. It is a discrete probability distribution. As an example suppose you are tossing a coin many times till you get heads. The probability of getting heads in a particular toss is independent of how many tosses you have made before that.