Fitting of Binomial Distribution

Suppose a random experiment consists of n trials, satisfying the conditions of Binomial distribution, and suppose this experiment is repeated N times. Then the
frequency of r successes is given by the formula, N\times P(r) = N\times {n\choose r}p^rq^{n-r}

Putting r = 0, 1, 2, …, n we get the expected or theoretical frequencies of the Binomial distribution, which are given in the table below.

Fitting of the binomial distribution means that we try to obtain the frequency distribution of the given data set assuming that it follows the binomial distribution. Thus we will obtain a new frequency distribution known as the fitted distribution for the given data set.

If p, the probability of success which is constant for each trial is known, then the expected frequencies can be obtained easily as given in the above table. However, if p is not known and if we want to fit a binomial distribution to a given frequency distribution, we first find the mean of the given frequency distribution by the formula, \bar{x}= \sum fx/\sum f and equate it to np, which is the mean of the binomial probability distribution.

Hence, p can be estimated by the relation, \bar{x} = np \implies p = \frac{\bar{x}}{n}.Then q = 1 – p. With these values of p and q, the expected or theoretical binomial frequencies can be obtained by using the formulae given in the above table.

Example of Fitting a Binomial Distribution:

We will fit the binomial distribution to the following set of data:

Here, n=4 and N= \sum f= 150. Then we find the mean of the distribution as follows, \bar{x}= \frac{\sum fx}{\sum f} = \frac{0 + 62 + 92 + 30 + 16}{150} = \frac{200}{150} = \frac{4}{3}.

The binomial probabilities are given by, P(r) = {n\choose r}p^rq^{n-r} = . The expected frequencies are given by the formula, N\times P(r) = N\times {n\choose r}p^rq^{n-r}

Substituting r=0, 1, 2, 3, 4 in the above formula we obtain the below table,

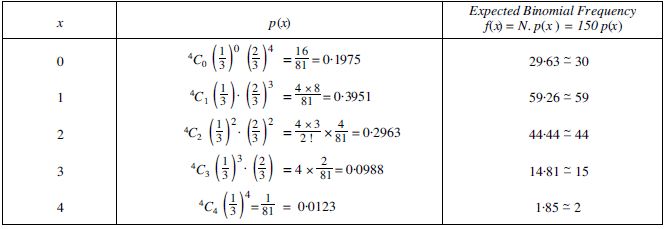
The above table shows the fitted binomial distribution for the given data set.