The mode of the binomial distribution is the value of X which maximizes the value of the binomial probability mass function. Thus if X = r is the mode then we should have p(r) > p(r – 1) and p(r) > p(r + 1).
How to find the Mode of the Binomial Distribution?
Let X be a Binomial variate with parameters n and p.
Case 1: When (n+1)p is an integer
Let (n + 1) p = k (an integer).
In this case, the distribution is bi-modal, the two modal values being X=k and X=k–1.
Example: Suppose n = 9 and p = 0·4, then (n + 1) p = 10 × 0·4 = 4, which is an integer.
Hence, in this case, the distribution is bi-modal, the two modal values being 4 and 4 – 1 = 3.
Case 2: When (n+1)p is not an integer
Let (n + 1)p = k + f, where k is the integral part and f is the fractional part of (n + 1)p. In this case, the distribution has a unique mode at X = k, the integral part of (n + 1) p.
Example: If n = 7 and p = 0·6, then (n + 1) p = 8 × 0·6 = 4·8.
Hence the distribution is unimodal and Mode = 4, the integral part of 4·8.
Proof of Mode of Binomial Distribution:
We want to find where the maximum value of the probability distribution function is attained. The probability distribution function of the binomial distribution is given as,
p(x) = P(X=x) = nCxpxqn-x.
We first calculate the ratio p(x)/p(x-1). We then divide our proof into two cases. We first deal with the case when (n+1)p is not an integer.
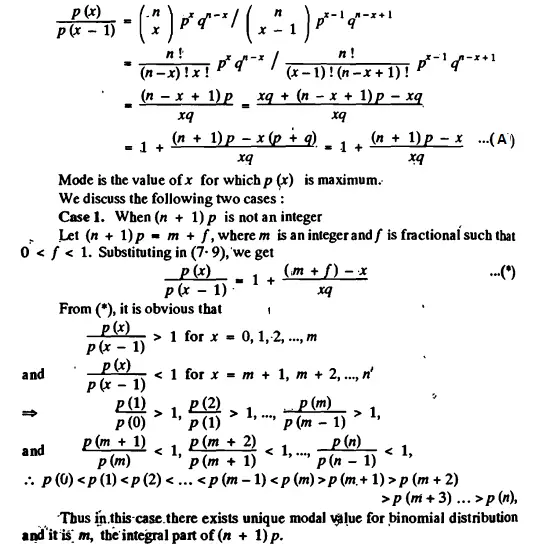
We now deal with the case where (n+1)p is not an integer. We have two modes in this case.
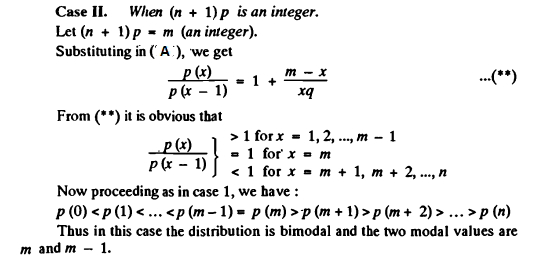
How many modes does the Binomial Distribution have?
The binomial distribution is either unimodal or bimodal depending on the value of the parameters of the distribution.
If (n+1)p is an integer then the binomial distribution has two modes equal to X=(n+1)p and X=(n+1)p+1.
If (n+1)p is not an integer then the binomial distribution has a unique mode equal to the greatest integer less than (n+1)p.
Is Mean and Mode equal for Binomial Distribution?
If np is a whole number (i.e., integer), then the distribution is unimodal and the mean and mode are equal each being np.
What is the Mode in Bernoulli Distribution?
If the value of p is equal to 0.5, then the Bernoulli distribution is bimodal and the values of the mode are equal to 0 and 1.
If the value of p is not equal to 0.5 then the Bernoulli distribution is unimodal and the mode is the value of X corresponding to the value greatest among p and (1-p).