Two Point Distribution – Definition & Examples

The Two Point Distribution refers to a probability distribution of a discrete random variable that can take two different values with certain probabilities.

The random variable can only take these two values and therefore the probability of taking any other value is equal to zero.

Probability Distribution of Two Point Distribution:

We say that a random variable X has two point distribution if it takes two values x₁ and x₂ with the probabilities given as,

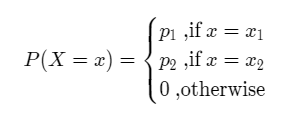
Note that the total probability is equal to 1, that is, p₁ + p₂ = 1.

The cumulative distribution function F(x) is given as,

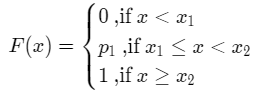
Mean and Variance:

The mean of the random variable X is E[X] = x₁p₁ + x₂p₂.

The variance of the random variable X is V[X] = p₁(1-p₁)(x₁-x₂)².

Raw moments:

The raw moments of the distribution are

E(X^m) = x₁^mp₁ + x₂^m(1-p₁) for m = 1, 2, 3,…

Moment Generating Function:

The moment generating function of the distribution is

M_X(t) = p₁e^tx₁ + (1-p₁)e^tx₂.

Bernoulli Distribution:

The Bernoulli distribution is a special case of a two-point distribution. We say that the random variable follows the Bernoulli distribution if it takes the values 1 and 0 with probabilities p and (1-p).

When x=1, we say that success occurs and when x=0, we say that failure occurs. For example, when tossing a coin only two outcomes are possible – heads (success) or tails (failure) each with probability 1/2. In this case, the random variable follows the Bernoulli distribution.

The sum of random variables following the two point distribution does not have the two point distribution.

For example, we know that the Bernoulli distribution is a two point distribution. But the sum of two i.i.d Bernoulli distributions follows the binomial distribution. The binomial distribution is clearly not a two point distribution.

Examples:

1. Suppose we toss an unbiased coin. Let X be the random variable that takes the value 1 when heads occur and takes the value 0 when tails occur. Then X follows a two-point distribution, in fact, the Bernoulli distribution with p=1/2.
2. Let X be a random variable that takes the value 1 if the number on a dice thrown is less than 3 and takes the value 0 when the number on the dice is greater than or equal to 3. Then X follows a two point distribution with p = 2/6 = 1/3.