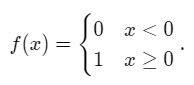A piecewise continuous function is a function that is continuous on every point of the domain of the function – except at a finite number of points.
Also, a piecewise continuous function is well-defined at every point meaning that it does not go to infinity at any point in its domain.
Intuitively speaking, this means that it is possible to draw the graph of the function without lifting the pen tip from the paper – except some finite number of times at the points of discontinuity.
We now give three examples of piecewise continuous functions and their graphs below.
Example 1:
Consider the function defined on the whole of the real line as follows,
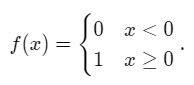
The graph of the function looks like follows,
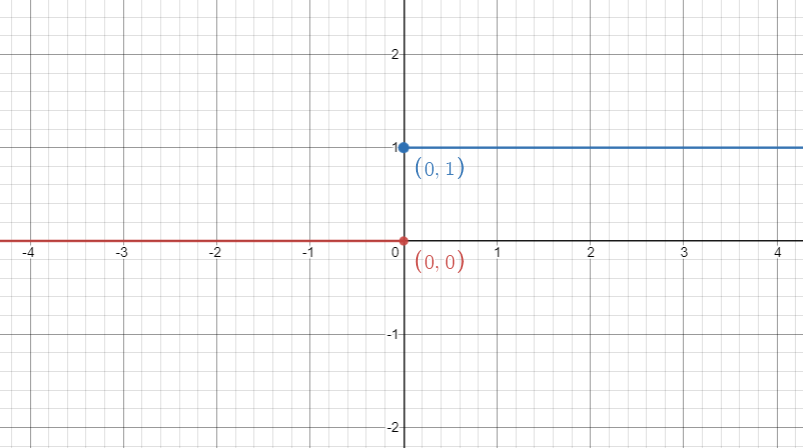
From the graph above it is evident that the function is continuous everywhere except at the point x=0.
Thus the above function is an example of a function with a single point of discontinuity.
Example 2:
We now give an example of a piecewise continuous function with two points of discontinuity. Consider the real valued function defined as
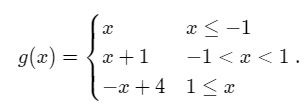
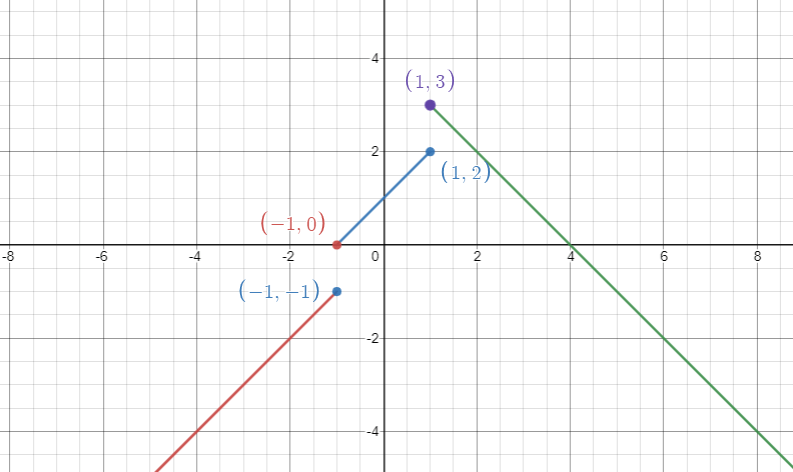
The above function has two points of discontinuity. When drawing the graph of this function a person must lift their pen tip from the page twice – at the points x=-1 and x=+1.
Example 3:
We now finally give an example of a function with three points of discontinuity.
Consider the following step function which remains constant except for jumps at the points x=-2, x=0, and x=2. The function is given as,
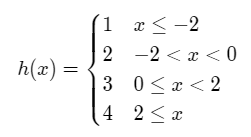
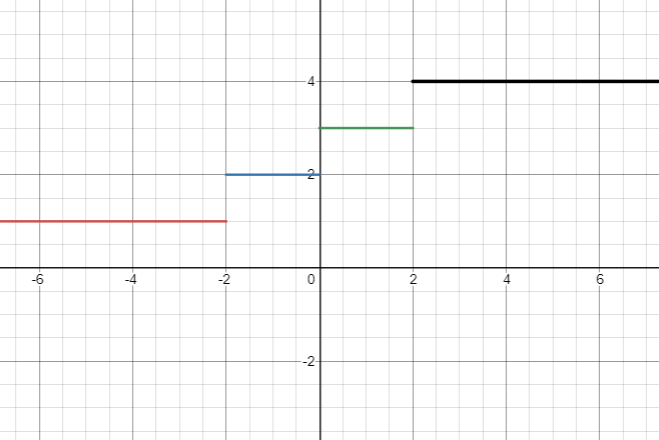
A function that is NOT Piecewise Continuous:
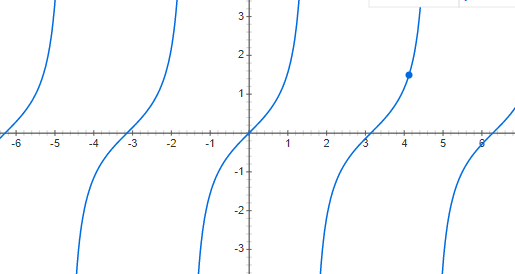
Consider the function f(x) = tan(x) defined on the entire real line. This function is continuous except at the points where it blows up to infinity. The function is not well defined at the points where it blows up to infinity.
Since it has infinitely many points of discontinuity and it blows up to infinity we see that the trigonometric function tan(x) defined on the real line is NOT a piecewise continuous function.