The mode for a given set of data refers to the data value that occurs with the highest frequency among the given data values. When we are given the data in ungrouped form, calculating the mode is particularly easy.
Simply count how many times each value occurs and the value occurring the highest number of times is the mode.
However, we cannot find the mode in this way if the data is given to us in the form of grouped class intervals.
In such cases, we use a formula to calculate the mode for the grouped data. In this article, we explain how to calculate the mode when data is given in the form of a grouped frequency distribution table.
Mode of Grouped Data Formula:
The mode for grouped data values can be calculated using the formula,
Mode = L + W * (f1-f0)/(2f1-f0-f2).
- Here W = width of the modal class
- L = lower bound of the modal class.
- f1 = frequency of modal class.
- f0 = frequency of class before the modal class.
- f2 = frequency of class after the modal class.
How to Find Modal Class and Calculate Mode for Grouped Data:
- Identify the class interval with the highest frequency. This class interval is known as the modal class. The mode lies in this class interval. The value of the highest frequency is denoted as f1.
- Find the width of the modal class by subtracting the lower limit from the upper limit. For example, if the modal class is 25-30, then the width is equal to 5. Let W be the width of the modal class and let L denote the lower bound of the modal class.
- Look at the class interval just before the modal class. Denote the frequency of this class interval as f0.
- Look at the class interval just after the modal class. Denote the frequency of this class interval as f2.
- Find the value of the mode using the formula below.
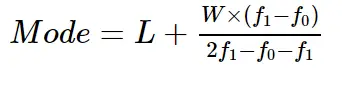
Solved Example 1:
Consider the following data about marks obtained by 60 students in an exam.
| Marks Obtained (Class Interval) | Number of Students (Frequency) |
| 0-10 | 9 |
| 10-20 | 7 |
| 20-30 | 14 |
| 30-40 | 11 |
| 40-50 | 9 |
Step 1: Since the highest frequency is f1=14, the modal class is 20-30. Hence the width is W=30-20 = 10 and the lower limit is L=20.
Step 2: The frequency of the class interval before the modal class is f0=7.
Step 3: The frequency of the class interval after the modal class is f2=11.
Step 4: Substitute the above values in the formula below to obtain,
Mode = L + W * (f1-f0)/(2f1-f0-f2).
Mode = 20 + 10 * (14-7)/(2*14-7-11) = 20 +7 =27.
So, we conclude that the mode of the marks obtained by the students in the exam is 27 marks.
Solved Example 2:
We can calculate the mode for the following grouped frequency distribution table:
| Class Interval | Frequency |
| 0-10 | 3 |
| 10-20 | 8 |
| 20-30 | 11 |
| 30-40 | 13 |
| 40-50 | 6 |
| 50-60 | 2 |
| 60-70 | 1 |
Here the highest frequency is f1 = 13, so the modal class is 30-40.
The lower limit of the modal class is L=30.
The size of the modal class is W=10. Also, f0=11 and f2=6.
Substituting all these values into the above formula we get that,
Mode = L + W * (f1-f0)/(2f1-f0-f2).
Mode = 30 + 10*(13-11)/(2*13-11-6) = 30 +20/9 = 30 + 2.2222 = 32.2222.
How to Find Mode for Ungrouped Data?
In order to find the mode for ungrouped data we simply check which data value has the highest frequency. For example, consider the following set of data values:

In the above example, the highest occurring frequency is 10. Hence the corresponding X value is the mode.
We conclude that the mode is equal to 13.