It is a fact that matrix multiplication is NOT commutative in general. This means that we may get a different result depending on the order in which the matrices are multiplied, that is, AB≠BA.
There are special kinds of matrices called scalar matrices which commute with every other matrix.
This means that matrix multiplication is commutative when one of the matrices is a scalar matrix. Scalar matrices are diagonal matrices where all diagonal entries all equal.
Why is Matrix Multiplication is Non-Commutative:
Consider the following two matrices.
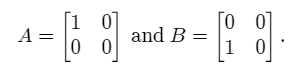
We now calculate the product AB.
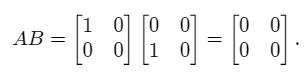
On the other hand, the product BA is equal to the following.
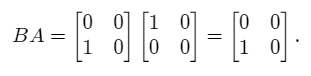
We see that AB is not equal to BA which shows that matrix multiplication is not commutative in general.
In order to find more counterexamples, we can try to consider two general 2 x 2 matrices and check when the two products are equal. Consider the two matrices
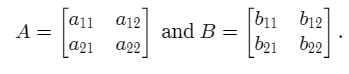
We now calculate the two products AB and BA.
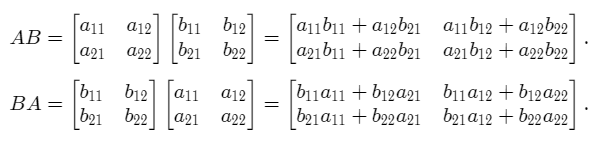
We see that the two products AB and BA are not equal in general.
Notice that if B is a scalar matrix of the form.
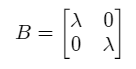
Then AB = BA holds and in this particular case, the matrix multiplication is commutative.