A matrix is nothing but a collection of numbers arranged in rectangular boxes. Hence a 1 x 1 matrix having only one row and one column is nothing but the scalar/number itself and the determinant is equal to the value of the scalar.
Example of a 1 x 1 matrix with a positive determinant:
Consider the matrix shown below.
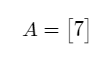
The above matrix has a determinant equal to 7.
Since the determinant is nonzero the equation Ax = 0 must have only the trivial solution.
This is clearly true since the equation 7x = has x = 0 as the only solution. This also gives us some motivation for why the determinant of a 1 x 1 matrix is defined in the manner above.
Example of a 1 x 1 matrix with determinant zero:
The matrix shown below clearly has a determinant equal to zero.
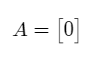
This means that the equation Ax = 0 must have a non-trivial solution. This is clearly true since the equation 0x = 0 is true for any value of x belonging to real numbers.
The determinant of the matrix A = [-4] is equal to -4.