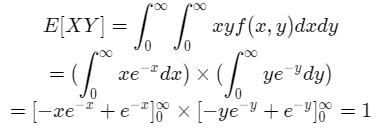The joint probability density function of X and Y is given as f(x,y)=e^-{x+y}

We give the solution to the following problem. Suppose that the joint probability density function X and Y is given as f(x,y)=e^-{x+y}. Then find:

1. P(X=Y)
2. P(min(X,Y)>1/2)
3. P(X ≤ Y)
4. the marginal density function of Y.
5. E[XY]

Solution:

We are given that X and Y have the following joint PDF,

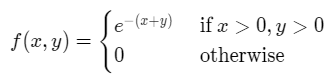
1) We define a new variable Z = X – Y. Since X and Y are random variables so is Z. Now, P(X=Y) = P(X-Y=0) = P(Z=0).

But we know that the probability of a random variable taking a simple point value is always zero. Therefore, P(Z=0) = 0 which is the required answer.

2) The minimum value of X and Y is greater than 1/2 if and only if both X and Y themselves take values greater than 1/2.

This is because if either X or Y were less than 1/2 then their minimum value would definitely be less than 1/2. Therefore we have,

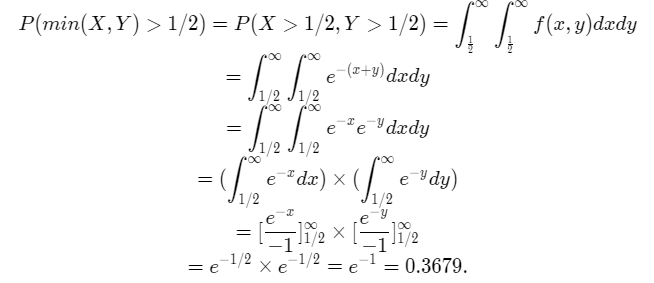
3) In order to calculate P(X ≤ Y), we let X vary between 0 and Y, whereas Y varies freely between 0 to infinity.

Therefore we have,

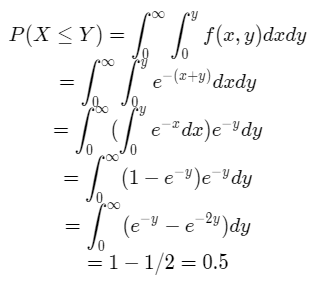
4) In order to find the marginal probability density function of Y, we integrate the joint PDF over the random variable X.

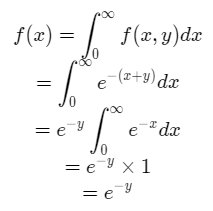
So the marginal density function of Y is,

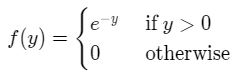
5) We use the formula,