It is a continuous probability distribution also known as the Lorentzian distribution. It looks similar to the normal distribution except that it has a relatively fatter end tail.
Its probability distribution function is given as,
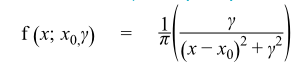
It has two parameters – the location parameter and the shape parameter. The location parameter tells us where the central peak of the distribution occurs. The scale parameter controls the slope and spread of the peak.
A Cauchy distribution with location parameter 0 and scale parameter 1 is called the standard Cauchy distribution. The standard Cauchy distribution coincides with the students t distribution with one degree of freedom.
An important fact about the Cauchy distribution is that the mean, standard deviation and other higher moments do not exist. This is because the integral that we use to calculate these quantities does not converge to a finite value.
Its median and mode exist and are equal to the location parameter.
If X and Y are normally distributed then the random variable X/Y follows the Cauchy distribution.
If X has standard Cauchy distribution then X2 follows the beta distribution.
Additive property of Cauchy distribution: If and X and Y are Cauchy random variables with location parameter ‘a’ and ‘b’ respectively and shape parameter ‘m’ and ‘n’ respectively then X+Y is also a Cauchy variate with location parameter ‘a+b’ and shape parameter ‘m+n’.
The Cauchy distribution is often used to calculate the probability that a spinning roulette comes to rest within a particular arc of a circle. It also finds application in finance where it is used to model high risk high valued investments.