Bivariate Normal Distribution – PDF & Examples

The bivariate normal distribution is a continuous joint distribution for two variables which when plotted looks like the three dimensional analogue of the “bell curve”. It is a generalization of a normal distribution for a single variate.

Formula for PDF of Bivariate Normal Distribution:

If two variables X and Y follow bivariate normal distribution then they are both distributed normally considered as separate random variables.

A more formal definition is that X and Y are jointly normally distributed if aX+bY is normally distributed for all a and b.

Another definition is in terms of their joint probability distribution function which looks like:

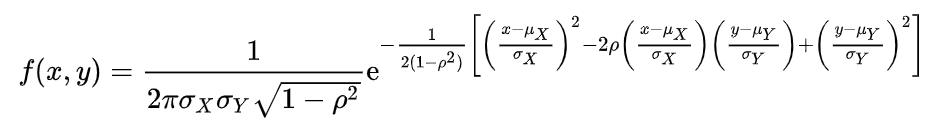
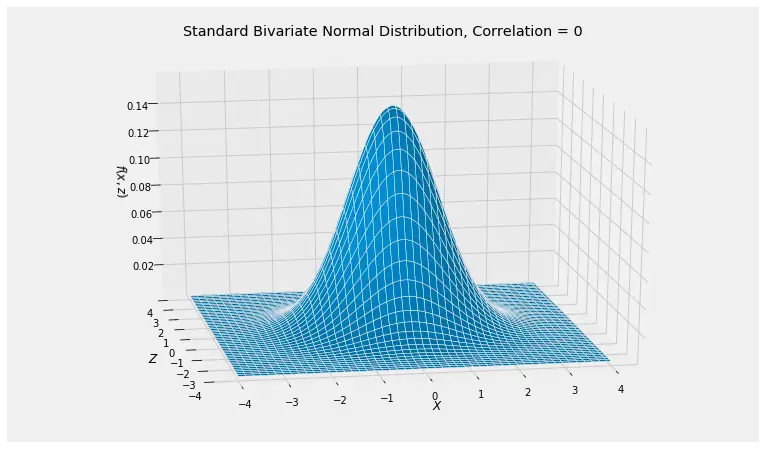
The parameter ρ gives the correlation between the two variables X and Y. If ρ=0 then the two variables are both independent. The bivariate normal distribution is a symmetric distribution.

It is a fact that if (X. Y) jointly follows bivariate normal distribution then the marginal PDFs of X and Y are also normal. However, the converse is not true. The marginal PDFs may be normal, but the joint PDF may not be normal.

Properties of Bivariate Normal Distribution:

1. It is generally used in situations where we have two variables that we know are distributed normally but there is some correlation between the two variables. For example, it is used to model the heights of a parent and their child which are definitely correlated and tend to be distributed normally.
2. The regression equations of Y on X and X on Y are linear and homoscedastic.
3. For  ρ=0, the conditional variance is equal to the marginal variance and the conditional mean is equal to the marginal mean and the two variables become independent, which is also apparent from the joint distribution function.
4. If X and Y are standard normal variates with a correlation coefficient ρ between them then the correlation coefficient between X² and Y² is given by ρ². Also, X+Y and X-Y are independent.

Multivariate Normal Distribution:

It is a generalization of the bivariate normal distribution when we have two or more random variables.

The variables X₁, X2,…, X_n are said to have multivariable normal distribution if a₁X₁+…..+a_nX_n is distributed normally for all a_i. Each of the variables is separately distributed normally, that is their marginal distribution is normal.

A similar kind of definition as above can be given in terms of the probability distribution function.

An example of a situation of a multivariate normal distribution would be if we were to jointly model the heights of a father, mother, and child.