Total Probability Rule

The total probability rule/theorem is used to calculate the probability of occurrence of an event when we are given the conditional probabilities of the event and marginal probabilities of mutually disjoint and exhaustive events.

Let P(B) denote the probability of occurrence of event B. The total probability rule/theorem states that,

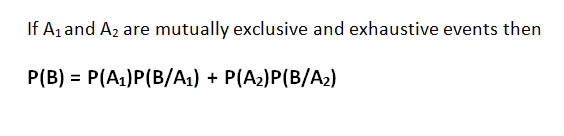
where, P(B/A₁) = conditional probability that event B occurs given that event A₁ has occurred

P(B/A₂) = conditional probability that event B occurs given that event A₂ has occurred

Let us understand how to apply the above formula by means of an example.

Example: Suppose a bag contains 5 red balls and 6 white balls. We choose two balls one after another. Calculate the probability that the second ball chosen is white.

Solution: We denote the events as follows,

A₁ – We pick the red ball at the first attempt

A₂ – We pick the white ball at the first attempt

B – We pick the white ball on the second attempt

Then clearly the marginal probabilities are,

P(A₁) = 5/11 and P(A₂) = 6/11

The conditional probabilities are,

P(B/A₁) = 6/10 because 6 white balls will be left if we pick a red ball at first attempt

P(B/A₂) = 5/10 because 5 white balls will be left if we pick a white ball at first attempt

Applying the total probability rule we get,

P(B)  = P(A₁) P(B/A₁) + P(A₂) P(B/A₂) = 5/11*6/10 + 6/11*5/10 = 60/110 = 0.5454

Total Probability Rule for more than two events:

We have a similar formula if we have more than two mutually exclusive and exhaustive events. In this case the formula is,

P(B)  = P(A₁) P(B/A₁) + P(A₂) P(B/A₂) +……+ P(A_n) P(B/A_n)

Here A₁,…..,A_n are the mutually exclusive and exhaustive events.