The class midpoint is defined to be the average of the upper and lower values of a given class interval. The class midpoint can be calculated using the formula,
Class Midpoint = (Upper class boundary + Lower class boundary)/2.
In a frequency distribution, another name for the midpoint of a class is the class mark.
The use of the class midpoint in a frequency distribution table is that it replaces a range of values with a single value. We can use the class midpoint and the frequency to construct a line graph for our data.
How to find Class Midpoint/Class Mark in a Frequency Table?
1) Note down the upper and lower limits for the first class interval.
2) Add the two values and then divide the result by 2, that is, take the average of the upper and lower class boundaries.
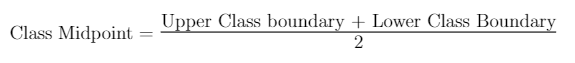
3) Repeat the procedure for each class interval and find all class midpoints.
4) An alternative way to find the class midpoint is to add half of the class width to the lower class interval.
Let us understand the above procedure by means of a simple example.
Example:
Consider the following grouped distribution table giving marks obtained in an exam vs the number of students in a class:
| Class intervals (Marks) | Frequencies (Number of students) |
| 0-10 | 7 |
| 10-20 | 12 |
| 20-30 | 13 |
| 30-40 | 3 |
| 40-50 | 5 |
The class mark/class midpoint for the first interval is calculated using the formula,
Class Midpoint = (Upper class boundary+ Lower class boundary)/2 = (0+10)/2 = 5.
We similarly calculate the class mark for each class interval and obtain the frequency table as follows,
| Class Mark/Class Midpoint | Frequencies (Number of students) |
| (0+10)/2 = 5 | 7 |
| (10+20)/2 = 15 | 12 |
| 25 | 13 |
| 35 | 3 |
| 45 | 5 |
Note that we could have found the class mark for 0-10 using the alternative way in Step 4 as well,
Class mark = Lower boundary + ½*Class width = 0 + ½*10 = 0+ 5 = 5.
Similarly, we can find the other class midpoints using the above alternative method. Notice that we will get the same result using this method.
Can the Class Midpoint be a Decimal?
The class midpoint can also take decimal values. Consider the following example:
| Class Interval | Frequency |
| 30-35 | 5 |
| 35-40 | 18 |
| 40-45 | 9 |
| 45-50 | 9 |
| 50-55 | 16 |
| 55-60 | 14 |
The class midpoint for the first interval 30-35 is:
Class Midpoint = (30 + 35)/2 = 65/2 = 32.5
Notice that the class midpoint is clearly a decimal value.
We can similarly find all class midpoints as shown below. As a shortcut, we can obtain the new class midpoint by adding the class width 5 to the previous class midpoint.
| Class Midpoint | Frequency |
| 32.5 | 5 |
| 37.5 | 18 |
| 42.5 | 9 |
| 47.5 | 9 |
| 52.5 | 16 |
| 57.5 | 14 |
Why is the Midpoint a Good Representative Value of each Class?
The class midpoint is a good representative value for each class since it is obtained by taking the average of the upper and lower class limits. It is equidistant from both the upper and lower class limits.
Since it is at an equal distance from both the upper and lower class limits we can say that it is truly the middlemost “average” value.
How to find Lower and Upper Class Limits using the Midpoint?
We can use the class midpoint and the class width to calculate the values of the upper and lower class limits. The upper and lower class limits can be calculated using the below formulae.
Upper Class Limit = Class Midpoint + 1/2*(Class Width).
Lower Class Limit = Class Midpoint – 1/2*(Class Width).
The Class Width refers to the length of the class interval.
For example, suppose that in a frequency distribution, we know that a given class has a class width of 10 and a midpoint of 35. We can determine the upper and lower limits as follows:
Upper Class Limit = Class Midpoint + 1/2*(Class Width) = 35 + 1/2*10 = 40.
Lower Class Limit = Class Midpoint – 1/2*(Class Width) = 35 – 1/2*10 = 30.
This means that the class interval is 30-40.
Notice that the class width is indeed equal to 10.