The zero product property states that if the product of two numbers is zero, then one of the two numbers has to be equal to zero. So if we are given two numbers a and b such that ab = 0 then we have that either a=0 or b=0.
Another way of stating the zero product property is that if you multiply two nonzero numbers then the product is guaranteed to be nonzero.
The main use of the zero product property is that we can apply the zero product property to solve equations where the product of two or more terms is equal to zero.
Let us understand this by looking at some examples.
Example 1: Solve the equation x2 – 36 = 0.
We first factorize the expression on the left-hand side as a product of two factors,
x2 – 62 = 0.
Using the identity a2 – b2 = (a-b)(a+b) we see that,
(x-6)(x+6) = 0.
Since the product of the two terms (x-6) and (x+6) is zero we can apply the zero product property to conclude that one of these terms must be zero.
Therefore, we have that either (x-6)=0 or (x+6)=0. Hence x=6 and x=-6 are the two solutions of the above equation.
Example 2: Solve the equation, x2 – 7x + 15 = 3.
We subtract 3 on both sides in order to obtain 0 on the right-hand side of the equation.
x2 – 7x + 12 = 0.
We then split -7x as the sum of -4x and -3x since the product of -4 and -3 equals +12. So we have that,
x2 – 4x – 3x + 12 = 0 ⇒ x(x-4)-3(x-4) = 0 ⇒ (x-4)(x-3) = 0.
We can now apply the zero product property to conclude that one of the terms (x-4) and (x-3) must be zero. Therefore, x=4 and x=3 are the two solutions of the given equation.
Zero Product Property for Matrices:
The zero product property does not hold for general algebraic systems. For example, it is known that the zero product property does not work in the case of matrix multiplication.
Consider the two matrices,
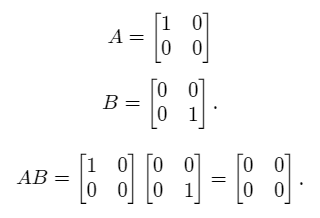
We see that the product of the two matrices is equal to the zero matrix even though matrices A and B are both nonzero.