In this article, we answer some common questions related to the notion of sample space in probability theory.
Question 1: What is a sample space in mathematics?
Answer: A sample space in mathematics refers to the collection of all possible outcomes of a random experiment. For example, when a dice is thrown the sample space is {H, T} because there are two possible outcomes – heads or tails. Another example is when a dice is thrown then the sample space is {1, 2, 3, 4, 5, 6}.
Question 2: What are all the events in the sample space that are not part of the specified event called ?
Answer: The events in the sample space that are not part of the specified event are called the complement of that event. For example, suppose a single dice is thrown. Let A be the fixed event that we get an odd number (1, 3, or 5). Then the complement of that event denoted as Ac (read “A complement”) is the event that we get an even number on the dice (that is we get either 2 or 4 or 6).
Similarly, if A is the fixed event that we get a number less than 3 (either 1 or 2) then the complement of that is we get a number greater than or equal to 3 (either 3 or 4 or 5 or 6). In a certain sense, the complement of a fixed event is the “opposite” of that event. The complement is the collection of those outcomes where A does not happen.
Question 3: What is a subset of outcomes of the sample space called?
Answer: A subset of outcomes of the sample space is called an event. For example, when two dice are thrown the sample space is {HH, HT, TH, TT}. Consider the subset P = {HH, HT, TH}. Then the subset P denotes the event that we get less than two tails.
For another example, consider the subset Q = {HT, TH}. Then the subset Q denotes the event that we get one head and one tail each.
Question 4: Find the sample space for tossing 2 coins. Then find P(exactly 1 head).
Answer: Let H denote the possibility that we get a head and let T denote the possibility that we get a tail. When two dice are thrown the sample space is {HH, HT, TH, TT}. The total number of outcomes is 4. If we get exactly one head then the favorable outcomes are {HT, TH}. The number of favorable outcomes is 2.
P(exactly one head) = Number of favorable outcomes/Total number of outcomes = 2/4 = 0.5.
Question 5: What is the set of probabilities associated with the values in a random variable’s sample space called?
Answer: The set of probabilities associated with the values in a random variable’s sample space is called a probability distribution.
The probability distribution is usually given in the form of a table that shows the outcome and the corresponding probability.
For example, when a dice is thrown each outcome has a one-sixth chance of occurring. The probability distribution table looks like this.
| Outcome on the dice | Probability |
| 1 | 1/6 |
| 2 | 1/6 |
| 3 | 1/6 |
| 4 | 1/6 |
| 5 | 1/6 |
| 6 | 1/6 |
Question 6: What is a sample space in mathematics?
Answer: A sample space in mathematics refers to the collection of all possible outcomes of a random experiment.
For example, when a dice is thrown the sample space is {H, T} because there are two possible outcomes – heads or tails. Another example is when a dice is thrown then the sample space is {1, 2, 3, 4, 5, 6}.
Question 7: What is the notation for sample space?
Answer: The sample space is a set and it is usually denoted by the letter S. The letter S is the symbol for the sample space. The specific events are then denoted by letters such as A, B, C, etc.
The outcomes inside the set are written inside curly brackets which is the usual set notation. For example, the sample space when a dice is thrown is S = {1, 2, 3, 4, 5, 6}.
Question 8: What is an element of the sample space called?
Answer: Each element of a sample space is called an outcome. For example, consider the event that a child is born. The sample space is {B, G} – boy or girl.
If a boy is born then that is one specific outcome and if a girl is born that is another specific outcome. Note that at least one of the outcomes in the sample space must occur when the random experiment is conducted.
Question 9: Which of the following is not an event when considering the sample space of tossing two coins?
- {HH, TT, HT}
- {HH, HT, TH, TT}
- {HH, HT}
- {HH, TT, HTH}
Answer: The event {HH, TT, HTH} is not possible when two coins are tossed. This means that {HH, TT, HTH} is not an event when considering the sample space of tossing two coins.
The third outcome HTH means that we have three coins with heads first, tails second, and heads third. This is clearly impossible since we are only allowing two coins, not three.
Question 10: An assignment of probabilities to events in a sample space must obey which three rules?
Answer: The following three important rules must be obeyed when assigning probabilities:
- The probabilities must sum to 1 when adding over all events in the sample space.
- The probability of any event must be a number between 0 and 1, inclusive.
- They must obey the addition rule for disjoint events.
For example, the probability distribution when a dice is thrown is given below.
Notice that in the below table, all the probabilities lie between 0 and 1. Also, the TOTAL of all the probabilities in the table below adds up to 1.
| Outcome on the dice | Probability |
| 1 | 1/6 |
| 2 | 1/6 |
| 3 | 1/6 |
| 4 | 1/6 |
| 5 | 1/6 |
| 6 | 1/6 |
| TOTAL = 6/6 = 1 |
Question 11: A coin is tossed 5 times in a row. What is the size of the sample space of this experiment?
Answer: Suppose that a coin is tossed five times. There are many possible outcomes, for instance, we may get three heads first followed by two tails – HHHTT.
There are 2 possible outcomes for the first try – H or T. Similarly, there are 2 possible outcomes for each of the second, third, fourth, and fifth tries.
We use the multiplication rule to find the total number of outcomes. We can find the total number by multiplying the possible number of outcomes for each of the 5 tries.
Therefore we have that, Size of Sample Space = 25 = 32.
There are a total of 32 possible outcomes.
Question 12: A useful graphical method of constructing the sample space for an experiment is :
- An ogive.
- A pie chart.
- A histogram.
- A tree diagram
Answer: The correct answer is a tree diagram. The tree diagram is a very useful way of visualizing all the possible outcomes of an event which will give us the sample space.
For example, when three coins are tossed the outcomes can be visualized in the tree diagram shown below.
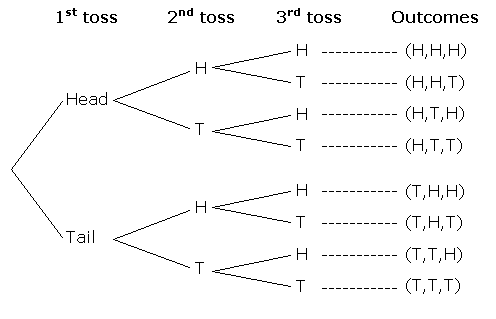
Question 13: You randomly choose a ball from a bag having four different colored balls red, green, yellow, and blue. What is the sample space?
Answer: The sample space is simply the collection of all possible outcomes. When we choose a ball it can be either of the four colors.
So the sample space is Sample Space S = {R (RED), G (GREEN), Y (YELLOW), B (BLUE)}.
Question 14: What do you mean by the cardinality of a sample space?
Answer: The cardinality of a sample space simply refers to the number of all possible outcomes of that sample space.
For example when two coins are tossed the sample space is {HH, HT, TH, TT}. In this case, the cardinality of the sample space is 4.