Probability Generating Function – Definition + Examples

The probability generating function is a power series that gives us the probabilities associated with a discrete random variable.

Definition:

Let X be a discrete random variable that takes non-negative values 0, 1, 2,….etc. Let p_i=P(X=i) denote the probability that the random variable X takes the value ‘i’. Then the probability generating function (p.g.f) is a power series in ‘s’ (denoted P(s)) defined as,

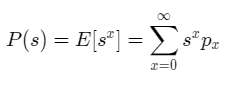
If we differentiate the above power series term by term ‘n’ times we get,

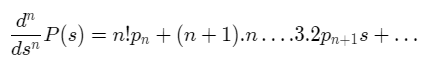
Substituting s=0 on both sides and rearranging terms we get,

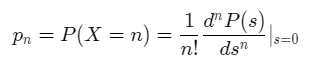
Thus we see that we can obtain the probabilities associated with a random variable by differentiating the probability generating function.

Examples of Probability-Generating Functions:

1. The probability generating function for the Poisson distribution with parameter λ is given as:

P(s) = e^-λe^sλ.

2. The probability generating function for the geometric distribution with parameter p is given as:

P(s) = p/(1-qs).

3. The probability generating function for the binomial distribution with parameters n and p is given as:

P(s) = (q+ps)ⁿ.

4. The probability generating function for the negative binomial distribution with parameters r and p is given as:

P(s) = (p/(1-qs))^r.

Properties of P.G.F:

• Let X and Y be two independent discrete random variables. Then the p.g.f of X+Y is equal to the product of their respective p.g.f’s, that is, P_{X+Y}(s) = P_X(s)P_Y(s).
• If the p.g.f is differentiated ‘r’ number of times, then on substituting s=1, we obtain the r^th factorial moment.
• If we substitute s=e^t in the p.g.f then we obtain the moment generating function of our random variable.