In this article, we explain how and why the range is not a resistant measure of spread. The range as a measure of dispersion is greatly affected by the presence of outliers. This means that the range is not a robust measure of the dispersion of the data.
Range is not a Resistant Measure of Spread:
We say that a quantity is a resistant measure of spread if it does not change abruptly if one of the values is replaced by an extreme value. The range is not a resistant measure of spread because if we replace one of the data values with an extremely large or extremely small value then the value of the range changes very drastically compared to the original value of the range. This means that the range is greatly affected by the presence of outliers in the data values. Let us try to understand this by looking at a small example.
Example:
The formula to calculate the range for a given set of data values is given as,
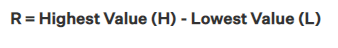
So we subtract the lowest value form the highest data value in order to calculate the range. Consider the following set of 10 data values,
11, 15, 15, 17, 19, 21, 22, 25, 29, 31
Here the highest and lowest values are,
Highest value H = 31
Lowest value L = 11
Hence we calculate the range to be equal to,
Range = Highest value – Lowest value = 31 – 11 = 20
What happens when we replace a value with an extreme outlier?
Now suppose that we were to replace the highest value 31 with an extremely large value such as 1001. Our new data values are as follows,
11, 15, 15, 17, 19, 21, 22, 25, 29, 1001
Then we can calculate the New range as follows,
New Range = Highest value – The lowest value = 1001 – 11 = 990
We see that the new value for the range(=990) is drastically different from the old value of the range which was equal to 20. Hence we conclude that mean is not a resistant measure of dispersion and is affected by outliers.