How to Check Linear Independence using Determinants (with Examples)

A collection of vectors is said to be linearly dependent if some non-trivial linear combination of them equals zero.

More formally, vectors v₁,v₂,…,v_n are said to be linearly dependent if there exist scalars a₁,a₂,…,a_n with at least one a_i nonzero such that,

a₁v₁+a₂v₂+…+a_nv_n = 0.

The vectors are said to be linearly independent if they are not linearly dependent. This means that:

If a₁v₁+a₂v₂+…+a_nv_n = 0 then a₁=a₂=…=a_n=0.

How to Check Linear Dependence:

1. We arrange the components of the vectors as rows of a matrix.
2. Calculate the determinant of the resulting matrix to check whether it is nonzero.
3. If the determinant is zero the vectors are dependent.
4. If the determinant is nonzero the vectors are independent.

Example 1:

Consider the three vectors as shown below.

a = (1, 0, 2).

b = (3, 4, -1).

c = (4, 4, 1).

Taking the components of the three vectors to be rows of a matrix we obtain the following matrix,

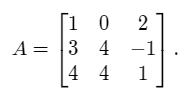
We now calculate the determinant of the above matrix.

det(A) = 1*(4 + 4) – 0*(3 + 4) + 2*(12 – 16) = 8 – 0 + (-8) = 0.

Since the determinant of the above matrix is zero we conclude that the three given vectors are linearly dependent.

This can also be seen very easily as follows,

(4, 4, 1) = (1, 0, 2) + (3, 4, -1).

c = a + b.

a + b – c = 0.

Since a non-trivial linear combination of the vectors is nonzero, this means that the vectors are linearly dependent.

This gives us another way of verifying linear dependence.

Example 2:

Consider the three vectors as shown below.

a = (3, 1, 0).

b = (0, -1, 2).

c = (4, 1, 2).

We now calculate the determinant of the above matrix,

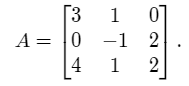
det(A) = 3*(-2 – 2) – 1*(0 – 8) + 0*(0 + 4) = -12 + 8 + 0 = -4.

Since the determinant is nonzero we conclude that the three vectors are linearly independent.