Two events are said to be disjoint (or mutually exclusive) if they cannot occur both at the same time. That is the probability of both of them occurring simultaneously is zero.
Given two events A and B we express this mathematically as,
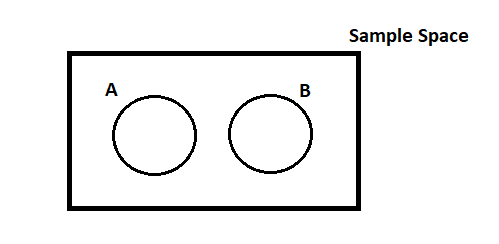
P(A∩B) = 0, that is, if we were to draw the sample space as a Venn diagram then events A and B would have no overlapping area between them as shown below.
Some examples of disjoint events are:
- Getting a head and getting a tail on a coin toss. You cannot have both; either you get a heads or a tails on flipping a coin.
- Getting a number greater than 5 on throwing a die and getting an odd number on throwing a dice. The occurrence of these two events together is impossible because the only number greater than 5 on a die is 6 which is not odd.
As we see in the above two examples two events are disjoint because they have contradictory conditions for occurring.
Disjoint events are also called mutually exclusive events because the occurrence of one ‘excludes’ the occurrence of the other event.
Some examples of events that are not disjoint are:
- Getting an odd number and getting a number less than 4 on throwing a die. These two events are not disjoint because both happen if we have a 1 or a 3.
- Getting an even number and getting a number that is prime on throwing a die. These two events are not mutually exclusive because both can occur if we get a 2 on the dice.
Complementary Events :
If two events are disjoint/mutually exclusive and cover all possible outcomes (exhaustive) then they are said to be complementary events.
For example, getting heads or getting tails on a coin toss are two complementary events because they are mutually exclusive and exhaustive (these are the only two possibilities in a coin toss).
Note that the probabilities of complementary events add up to one. If A and B are complementary events then P(A)=1-P(B).
