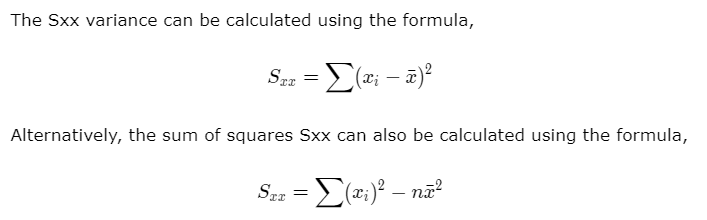The calculators below calculate the value of Sxx, Sxy, and Syy on the basis of the x data values and y data values entered. Simply enter the values of the x and y variables in the calculators below to find the Sxx, Sxy, and Syy values.
Sxx Calculator:
The Sxx value is calculated by adding up the squared deviations of the data values from the mean. The calculator below finds the value of Sxx on the basis of the x values entered.
Sxx: 49.71429
Sxy Calculator:
The Sxy variance can be found by taking the sum of the product of deviations of the x and y values from their means. We need to enter both the x and y data values in order to calculate the Sxy value.
x values:
y values:
Sxy = -291.00000
Syy Calculator:
The sum of squares due to Y, that is, Syy can be calculated using the formula,
Syy = Σ(Yi - Ȳ)2.
We can directly obtain the Syy value using the calculator below.
Syy: 317.42857
Example Calculation:
The Sxx value is an important quantity that is useful during calculations in both regression and correlation analysis. It is calculated using the formula,
Sxx = Σ (Xi - X̄)2
For instance, if the x values are 1, 2, 2, 3, 5, 8, and 9. Then,
Step 1: We first calculate the mean X̄,
X̄ = (2 + 3 + 6 + 8 + 3 + 8 + 9)/7 = 39/7 = 5.5714
Step 2: Then we calculate the x variance by subtracting the data values from the mean, squaring the differences, and then adding them up,
Sxx = Σ (Xi - X̄)2 = (2 - 5.5714)2 + (3 - 5.5714)2 + (6 - 5.5714)2+ (8 - 5.5714)2 + (3 - 5.5714)2 + (8 - 5.5714)2 + (9 - 5.5714)2 = 49.71429
As we see above, the calculations can be long and tiresome to perform by hand. We recommend that you use the Sxx calculator above to calculate the value directly without any manual calculations.