The Sxx value can be calculated using the formula,
Sxx = ∑(Xi – X̅)2.
The Sxx refers to the sum of squares due to the variable x in both linear regression and ANOVA. It basically measures the amount of variation introduced in the data because of the x variable.
Formula for Calculating Sxx:
The sum of squares due to x, that is the Sxx variance can be calculated using the equation,
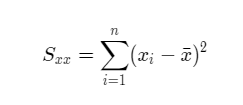
- Here xi denotes the given data values of the variable x.
- x̄ denotes the mean/average of the x data values.
- n denotes the number of given data values of the variable x. The sum is taken from i=1 to i=n.
Alternatively, the sum of squares Sxx can also be calculated using the formula,
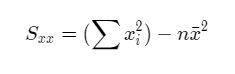
The alternative formula is obtained from the original formula by simply expanding the square and carrying out the algebraic simplifications.
The original formula and the alternative formula both give the same answer.
The advantage of the alternative formula is that the calculations are much easier to carry out by hand.
Example 1:
We now illustrate how to calculate Sxx for given data values using the original formula. Consider the following 5 data values:
3, 7, 12, 8, 5
We first calculate the mean of the given values,
x̄ = ∑xi/n = 3+7+12+8+5/5 = 25/5 =5
We then obtain the square of the differences as follows,
| xi | (xi – x̄)2 = (xi – 5)2 |
| 3 | (3-5)2 = (-2)2 = 4 |
| 7 | (2)2 = 4 |
| 12 | (7)2 = 49 |
| 8 | (3)2 = 9 |
| 5 | (0)2 = 0 |
| ∑ (xi – x̄)2 = 66 |
On summing up all the values in the last column, we see that the Sxx value is equal to 66.
Sxx= ∑ (xi – x̄)2 = 66
Example 2:
Next, we will see an example of how to calculate Sxx for given data values using the alternative formula. Consider the following 8 data values:
4, 6, 2, 7, 1, 10, 3, 7
We first calculate the mean of the given values,
x̄ = ∑xi/n = 4+6+2+7+1+10+3+7/8 = 40/8 =5
We then obtain the squares of the data values as follows,
| xi | xi2 |
| 4 | 42 = 16 |
| 6 | 36 |
| 2 | 4 |
| 7 | 49 |
| 1 | 1 |
| 10 | 100 |
| 3 | 9 |
| 7 | 49 |
| ∑ xi2 = 264 |
Using the alternative formula for Sxx we obtain that,
Sxx= ∑ xi2 – n* x̄2
Sxx = 264 – 8*(52) = 264 – 8*25 = 224
Is Sxx Equal to the Variance?
It is important to note that the Sxx value is not itself equal to the variance. But, we can use the Sxx value to calculate the value of the variance.
If we divide the Sxx value by the number of observations (n) we obtain the value of the variance.
For example, suppose that we are given n=8 number of observations and Sxx = 72. Then the variance of the data values is,
Variance = Sxx/n = 72/8 = 9