In probability theory, a sure event is an event that is always guaranteed to occur no matter the outcome of the random experiment. If A is a sure event then P(A) =1. A sure event that is bound to occur always has a probability equal to one.
Another definition of a sure event is an event such that the union of all possible outcomes of the event is equal to the sample space. Let us try to understand the definition by looking at some examples.
Example 1 – Rolling a single die:
Suppose we roll a die and the event A is defined as follows. Let A be the event that we either get an even number OR on an odd number. Then event A is a sure event because no matter what number we get on the die it can either be even OR odd. Now the outcomes where we get an even number are {2, 4, 6} and the outcomes where we get an odd number are {1, 3, 5}. We see that the possibilities for the occurrence of event A are {1, 2, 3, 4, 5, 6} which is clearly equal to the whole sample space.

Example 2 – Tossing two coins:
When tossing two coins let A be the event defined as – “We get at least one head OR at least one tail”. The possible outcomes when tossing two coins are:
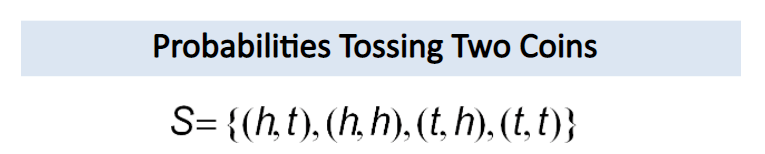
Suppose we get the outcome HH. Since we have 2 heads in this case we have satisfied the condition of getting at least one head. Since we either needed either one head or one tail we conclude that event A has occurred. Similarly, we can check that every other point in the sample space has at least one head or at least one tail. Thus, we conclude that A is a sure event.
Example 3 – Breakdown of an Electronic Device:
Since any electronic device has a date beyond which it stops functioning we can conclude that the eventual breakdown of any electronic device is bound to happen sooner or later. This is because it is impossible for an electronic device to keep functioning indefinitely. Thus the probability that an electronic device eventually stops working is 1.