The Spearman-Brown prediction formula tells us how the reliability of a test/questionnaire changes if we increase the number of questions in the test/questionnaire.
The Spearman Brown formula is given as,
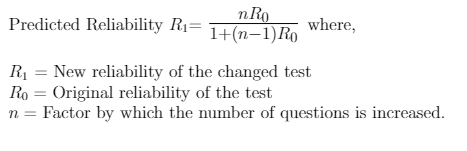
Spearman Brown Formula and Split Half Reliability:
The above formula can be used when we split a test into two halves. The split half reliability of a test is obtained by dividing the test into two equal parts. By substituting the split half reliability obtained in the above formula (putting n=2 since the original test has double the number of questions) we can obtain a score for the reliability of the original test.
Example: Suppose that the reliability score of a test is 0.7. If we increase the number of questions in the test by 4 times then what is the new reliability score of the test.
Solution: Given R0 = 0.7 and n=4
Substituting all these values in the above formula we get,
Predicted reliability R1 = 4*0.7/(1+3*0.7) = 0.903
Predicting the number of questions in the new test:
We can calculate the factor by which we need to increase the number of questions in order to achieve the desired reliability by using the formula,

Example: Suppose that the reliability score of a test having 100 questions is 0.8. If we want to increase the reliability of the test to 0.9 find the factor by which the number of questions must be increased.
Solution: Given R0 = 0.8 and R1 = 0.9
Substituting all these values in the above formula we get,
n = 0.9*(1-0.8)/0.8*(1-0.9) = (0.9*0.2)/(0.8*0.1) = 2.25
So we should increase the number of questions by a factor 0f 2.25 to obtain the desired reliability.
The new test should have 100*2.25 = 225 questions so that we can reach the desired reliability score of 0.9