How to Use Slovin’s Formula (with Examples)

Slovin’s Formula is used to determine what sample size should be chosen to study a given population given an acceptable margin of error. Slovins formula is given as:

n = N/(1 + Ne²).

• ‘n’ denotes the sample size.
• ‘N’ denotes the size of the population.
• ‘e’ denotes the maximum acceptable error.

Depending on the margin of error, we can use Slovin’s formula to decide the size of the randomly selected sample.

Slovins Formula – Example 1:

Suppose that a company wants to conduct marketing supply research to know about consumer preferences.

The company estimates that a total of N = 10000 people are regular loyal customers of the company.

How many of these people should be interviewed to understand customer preferences? Take the margin of error to be 5%.

Solution:

We want to choose a random sample of size ‘n’ from the entire population of customers. Applying Slovin’s formula we get that,

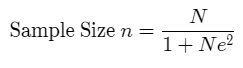
n = N/(1 + Ne²) =10000/(1 + 10000*0.05²).

n = N/(1 + Ne²) = 10000/26 = 384.61.

This means that a total of 385 people should be randomly selected and interviewed to conduct research on consumer preferences.

Slovins Formula – Example 2:

Suppose that the population size in a study is N = 5000 and the margin of error is 3%.

How many units should be chosen in a randomly selected sample?

Solution: By Slovin’s formula we get that,

n = N/(1 + Ne²).

n = 5000/(1 + 5000*0.02²).

n = 5000/3 = 1666.67.

This means that a total of 1667 units should be randomly selected.

How to Calculate Margin of Error in Slovins Formula?

The Margin of Error in the Slovins formula can be calculated as,

Margin of Error e = √[(N-n)/Nn].

• n is the sample size.
• N is the population size.

Margin of Error – Example 1:

Suppose that we want to find the average height of a city whose population is 10500. A researcher takes a random sample of 500 people in order to measure the average height.

What is the Margin of Error?

Solution: The Margin of Error is calculated as follows,

Margin of Error e = √[(N-n)/Nn] = √[(10500-500)/10500*500].

Margin of Error e = √[10000/(10500*500)] = √0.001904.

Margin of Error e = 0.0436.

So, the margin of error is around 4.36%.

Since a margin of error of less than 5% is usually acceptable, we conclude that the researcher has chosen a good sample size.

Margin of Error – Example 2:

Suppose that a researcher wants to study a population of a thousand people. He extracts a sample of size 100 randomly in order to conduct the statistical study.

What is the Margin of error?

Solution: The margin of Error can be calculated directly using the formula as in the above example.

Alternatively, it can also be calculated by substituting the values of the sample size and population size in Slovin’s formula and then solving for the margin of error. We have that,

n = N/(1 + Ne²).

100 = 1000/(1 + 1000e²).

100(1 + 1000e²) = 1000.

100 + 100000*e² = 1000.

100000*e² = 900.

e² = 9/1000.

Taking square roots on both sides we get,

e = 0.0948.

This means that the margin of error is around 9.48%.

The researcher should increase the sample size in order to reduce the margin of error below 5%.

Why do we Use Slovins Formula?

Suppose that you want to know about the voting preferences of a given population of a country.

It is not feasible to ask each and every person about their voting preferences.

In such a situation, it is reasonable to select a random sample from the entire population and interview only those people who are selected. But this introduces scope for error in the study.

We also need to decide how many people should be included in our sample. We can use Slovin’s formula to decide the sample size.

Remarks:

1. Slovin’s formula cannot be used to determine the sample size if the population size is very small.
2. Clearly, a larger sample will minimize the error and a smaller sample greatly increases the error rate. Generally, a 5% error rate is considered acceptable.
3. As a general rule, the sample size should be 20% of the given population for small population sizes (less than 500), and the sample size should be 10% of the given population for population sizes greater than 1000.