The error arising due to drawing inferences about the population on the basis of a few observations (sampling) is defined as sampling error.
The sampling error is non-existent if we carry out a complete enumeration survey but since this is not always possible we carry out sampling to study the population. This leads to the occurrence of sampling error.
Even if the sample has been chosen as carefully as possible, there is no guarantee that it completely and faithfully represents the original population.
The sampling error is the difference between a sample statistic and a population parameter. The sampling errors are divided into two kinds – Biased and Unbiased.
Biased Errors:
These errors arise from any bias in the selection of the sample, estimation, etc. For example, if in place of simple random sampling, the researcher deliberately introduces a sample point that he favors then that may lead to errors in the final result.
For example, when testing the effectiveness of a particular health regimen the researcher might deliberately introduce only relatively healthier individuals in order to demonstrate the effectiveness of the regimen.
The causes for the introduction of bias in the study are:
- Deliberate selection of a sample point.
- The unconscious bias of the researcher.
- Non-response bias – This means that the researcher receives no response to the mail/questionnaire sent to the individual.
Avoidance of bias: If there is a bias in our study then the conclusions cannot be trusted. Hence our first order of business must be to eliminate the bias.
The simplest and most certain way to eliminate bias is to select the process in a random manner using established techniques such as simple random sampling, stratified sampling, cluster sampling, etc.
When using stratified random sampling, the sampling error will be zero (that is the bias will be zero; there will still be some error due to the unbiased error).
Unbiased error:
These errors arise due to the chance differences between the members of the population included in the sample and those not included in the sample.
While we can remove the biased error from our study by improving the sampling methodology, we can never completely remove the unbiased error.
This is because unbiased error is purely a matter of chance. The unbiased error can be minimized by increasing the sample size.
Formula for Sampling error:
The sampling error can be calculated using the formula,
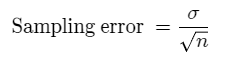
where σ is the standard deviation of the population and n is the size of the sample. The true sampling error is usually not known because the population standard deviation is not known.
We can estimate the population standard deviation by the sample standard deviation. Hence we can only obtain an estimate of the sampling error, while the true sampling error remains unknown.
Reducing Sampling Errors:
Once the bias has been removed, attention must be paid to the random sampling errors. Such errors must be minimized in order to attain greater accuracy.
The simplest way of increasing accuracy is to increase the size of the sample. As we can see in the above formula, as the value of ‘n’ increases the sampling error becomes smaller and smaller.
However, increasing the sample size leads to marginal gains after a certain point. Hence, we should use the optimum sample size for the desired level of accuracy.