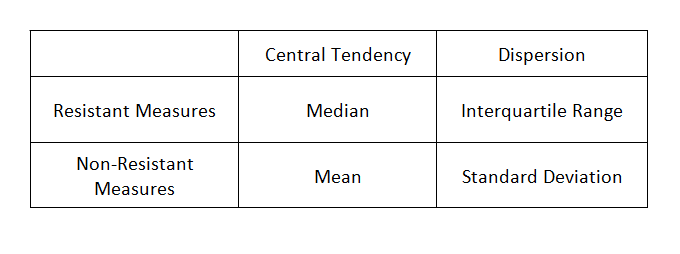
The resistant measures in statistics are those quantities that are resistant to outliers, meaning that they are not affected too much by the presence of an outlier in the data. The non-resistant measures are not resistant to outliers and hence change drastically depending on whether there are outliers in the data or not.
Some examples of statistical measures which are resistant to outliers are:
- Median
- Interquartile Range
The Median and Interquartile Range as resistant to outliers because they are calculated using values lying near the center of the data.
The extreme values such as the highest and lowest values in the data play no part in the calculation of the median or the interquartile range.
Some examples of statistical measures which are not resistant to outliers are:
- Mean
- Standard Deviation
- Range
They are not resistant to outliers because they are calculation involves using extreme values such as the highest and lowest values in the data. For example, if the largest value increases then the mean is also correspondingly increased.
The above information can be summarised in the following table:
Example:
Consider the following data values: 100, 200, 350, 400, 500
Without Outliers: We calculate the mean and the median and get that,
Mean = 1550/5 = 310
Median = 3rd term = 350
Now suppose the value 500 is replaced by an outlier say, 2000
Without Outliers: The new data values are: 100, 200, 350, 400, 2000
We calculate the new mean and the median and get that,
New Mean = 3050/5 = 610
New Median = 3rd term = 350
We see that the value of the mean changed drastically because of the outlier whereas the median was resistant to the presence of the outlier.
Sensitive Measures:
The measures such as mean and standard deviation which are not resistant to outliers are sometimes also called sensitive measures.
This is because these quantities are highly sensitive to any change in the data and get drastically affected by the presence of outliers.