Reliability Theory is a branch of statistics that deals with the study of determining probabilities of failure of objects and systems comprising of a number of components.
The reliability of the system of course depends on the reliability of the components. The reliability of a system/object is the probability that the system/object does not fail before a given time.
How do we model the reliability of an object?
The reliability of an object can be calculated using a probability distribution. Generally speaking distributions like the exponential distribution, Weibull distribution, and other decaying-type distributions are used to model the reliability of the object.
The probability of failure before the time ‘t’ is denoted as F(t). Then, R(t)=1-F(t) called the reliability function is the probability that the object does not fail before time ‘t’.
The function F(t) is the cumulative distribution function of the pdf (probability distribution function) denoted by f(t). As stated above the pdf is taken to be either the exponential or the Weibull distribution.
The quantity λ(t)= f(t)/R(t) is called the failure rate. We can use the failure rate to calculate the mean time to failure (MTTF) given by the formula,

Rules to calculate the reliability of a system:
- To calculate the reliability of a system we need to consider the reliability of the components and calculate the probabilities depending on whether the objects are connected in series or parallel.
- If the components are connected in series then we multiply the probabilities of survival of the components.
- If the components are connected in parallel then we multiply the probabilities of failure of the components.
Example:
Consider the below circuit consisting of five components A, B, C, D, and E. The probability that each of these components fails within a year is 0.1,0.2,0.15,0.1 and 0.1 respectively. Calculate the probability that the circuit fails within a year.
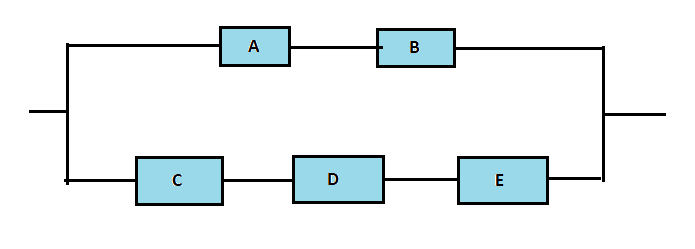
Solution: We use P(A) to denote the probability of occurrence of event A
Step 1: Clearly P(circuit fails)= P(upper branch fails )*P(lower branch fails) as per rule 3 above and therefore we need to calculate the probabilities of failure of individual branches.
Step 2: Now P(upper branch survives)
= P(component A survives)*P(component B survives)
= [1-P(component A fails )]*[1-P(component B fails)]
=(1-0.1)*(1-0.2)=0.72
Step 3: Similarly P(lower branch survives)
= P(component C survives )*P(component D survives)* P(part E survives)
=(1-0.15)*(1-0.1)*(1-0.1)=0.6885
Step 4: Since failure is a complement to survival, therefore, the failure probabilities of both branches can be obtained by subtracting survival probabilities from 1.
Hence P(circuit fails)= P(upper branch fails )*P(lower branch fails)
=(1-0.72)*(1-0.6885) = 0.08722=8.722%
Answer: We conclude that there is an 8.72% chance that the circuit fails within a year.