How to find Quartiles for Grouped Data (with Examples)

The quartiles for grouped data can be calculated using the formula,

Q_i = L + h/f*(iN/4 – c.f).

• The class containing Q_i is the class whose cumulative frequency is just greater than (iN/4).
• N = Total Frequency.
• h = class size.
• L = lower limit of the class containing Q_i.
• f = frequency of the class containing Q_i.
• c.f = cumulative frequency of the class interval preceding the interval containing Q_i.

The three quartiles are numerical values that divide the given data into four equal parts.

The lower quartile, the median, and the upper quartile divide the data at the one-fourth, one-half, and three-fourths values respectively. They are denoted by the symbols Q₁, Q₂, and Q₃.

Steps to find Quartiles for Grouped Data:

1. Find the value of N, by adding up all the frequencies.
2. Calculate the less than cumulative frequencies for all class intervals.
3. Calculate the value of (iN/4) in order to find the i^th quartile (i = 1, 2, or 3).
4. The quartile is contained in the class whose cumulative frequency is just greater than (iN/4).
5. Calculate the value of the i^th quartile by using the formula given below.

Example 1:

Calculate the upper quartile Q₃ for the following grouped frequency distribution:

Solution: Since we want to calculate Q₃ we have that i=3 in the above formula.

We first calculate the less than cumulative frequencies by adding up the current and preceding frequencies of a class interval.

Now, since i=3 we have that (iN/4) = (3*20/4) = 15.

The value of cumulative frequency just greater than 15 is 18.

Therefore, Q₃ lies in the class interval 30-40. Here, L = 30, f = 5, h =10 and c.f = 13.

We substitute all these values in the above formula.

Q₃ = L + h/f*(3N/4 – c.f).

Q₃ = 30 + 10/5*(3*20/4 – 13).

Q₃ = 30 + 2*(15 – 13) = 30 +4 =34.

Example 2:

Calculate the lower quartile Q₁ for the following grouped frequency distribution:

Solution: Since we want to calculate Q₁ we have that i=1 in the above formula.

Now, since i=1, we have that (iN/4) = (1*28/4) = 7.

The value of cumulative frequency just greater than 7 is 15. Therefore, Q₃ lies in the class interval 5-10.

Here, L = 5, f = 10, h =5 and c.f = 5. We substitute all these values in the formula.

Q₁ = L + h/f*(N/4 – c.f).

Q₁ = 5 + 5/10*(28/4 – 5).

Q₁ = 5 + 1/2*(7-5) = 5+1 =6.

Therefore the value of the lower quartile is 6.

Calculating Quartiles Graphically:

1. Draw a cumulative frequency curve by plotting the values of observations or class intervals along the horizontal scale (i.e. x-axis) and cumulative frequency along the vertical scale (i.e., y-axis).
2. Determine the quartile value, that is, the value of (in/4)^th observation (i = 1, 2, 3), where n is the total number of observations in the data set.
3. Locate this value on the y-axis and from this point draw a line parallel to the x-axis meeting the ogive at a point, say P. Draw a perpendicular on the x-axis from P and it meets the x-axis at the point, say M. Then M is the required value of the quartiles.

Example:

Consider the data given in the form of a grouped frequency distribution as follows:

We first calculate the cumulative frequencies by adding each frequency value with the preceding frequencies.

Let us calculate the value of the second quartile, that is, the median. We have that,

Second Quartile = (iN/4)th term = (2*600/4)th term = 300^th term.

We now construct the cumulative frequency curve (ogive) and locate the second quartile as follows.

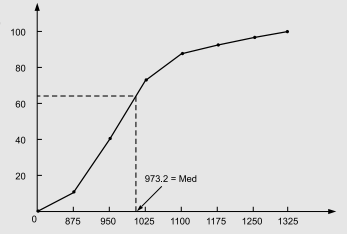
Therefore the value of the second quartile is 973.2

Summary

Article Name

The quartiles for grouped data can be calculated using the formula,

Description

The quartiles for grouped data can be calculated using the formula, Qi = L + h/f*(iN/4 - c.f). The class containing Qi is the class whose cumulative frequency is just greater than (iN/4). N = Total Frequency. h = class size. L = lower limit of the class containing Qi. f = frequency of the class containing Qi. c.f = cumulative frequency of the class interval preceding the interval containing Qi.