On an ordinary graph, the X-axis and the Y-axis divide the graph into four equal parts. These 4 parts are the quadrants on a graph. The image below shows the labeled quadrants:
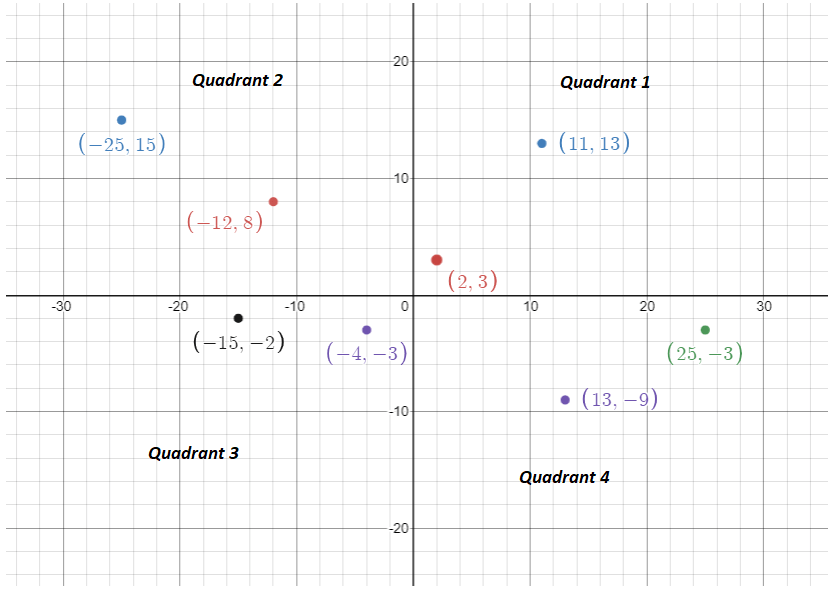
As we can see in the above image, the upper-right quadrant is labeled as Quadrant 1. It is also known as the first quadrant. The other quadrants are numbered/labeled in ascending order in an anti-clockwise manner.
- The 1st Quadrant/Quadrant 1 contains those points whose x and y co-ordinates are both positive. For example, the point (2,3) and (11,13) lie in the first quadrant. This can be seen in the above image. The first quadrant lies on the upper-right side of the graph.
- The 2nd Quadrant/Quadrant 2 contains those points whose x co-ordinate is negative and y co-ordinate is positive. For example, the point (-12,8) and (-25,15) lie in the second quadrant. The second quadrant lies on the upper-left side of the graph.
- The 3rd Quadrant/Quadrant 3 contains those points whose x and y co-ordinates are both positive. For example, the point (-4,-3) and (-15,-2) lie in the third quadrant. The third quadrant lies on the lower-left side of the graph.
- The 4th Quadrant/Quadrant 4 contains those points whose x co-ordinate is positive and y co-ordinate is negative. For example, the point (25,-3) and (13,-9) lie in the fourth quadrant. The fourth quadrant lies on the lower-right side of the graph.
Remarks:
- Each quadrant covers an angle of 90 degrees on the graph. So all the four quadrants add upto a total of 360 degrees which covers the entire graph.
- The origin (0,0) lies exactly at the center of the graph. It is considered to belong to each of the four quadrants.
- Consider the point (4,0) which lies on the x-axis. If we plot the point on the graph we see that it lies in both the first and the fourth quadrants. So we see it is possible that a point lies in two quadrants at the same time.
