Suppose we are given a line AB. The perpendicular bisector of the given line is a line that divides the line AB into two equal parts (“bisector”) and forms an angle of 90 degrees (“perpendicular”) with the given line AB.
How to Draw the Perpendicular Bisector of a given line:
The process used to draw the perpendicular bisector of a given line is as follows:
Step 1: Suppose that we are given a line segment of some length. We first label the endpoints of the line segment as A and B for ease of reference. We should also get hold of a ruler and compass required for our construction.
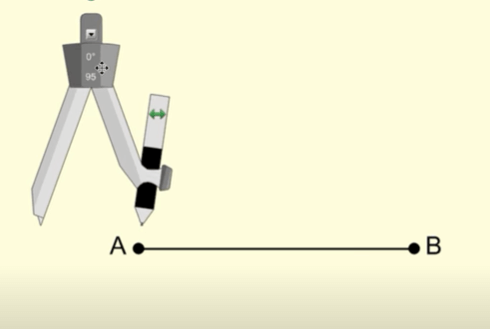
Step 2: Set the endpoint of the compass needle at point A. Extend and open up the compass so it covers roughly more than half of the line segment.
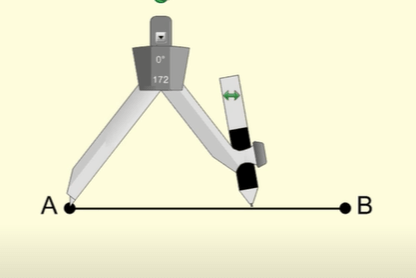
Step 3: With point A as the center draw a circular arc as shown below.
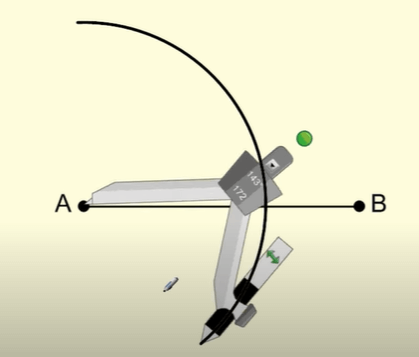
Step 4: Without changing the radius of the compass we now set the endpoint of the compass needle to point B.
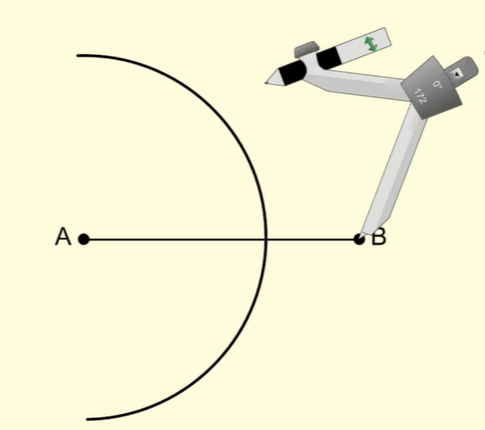
Step 5: With point B as the center draw a circular arc as shown below.
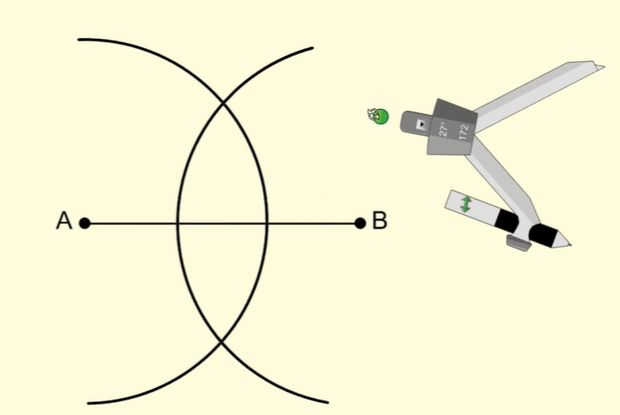
Step 6: Label the two points of intersection as C and D.
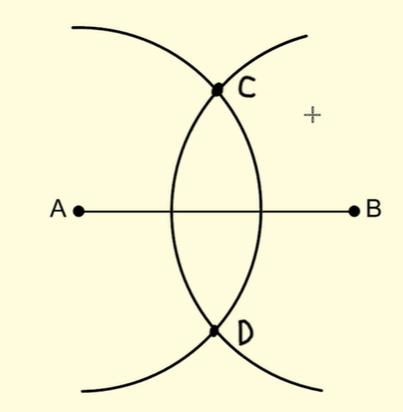
Step 7: Join the two points C and D by using a ruler/straightedge. The resulting line segment so obtained is the perpendicular bisector. It divides line AB into two equal halves at an angle of 90 degrees.
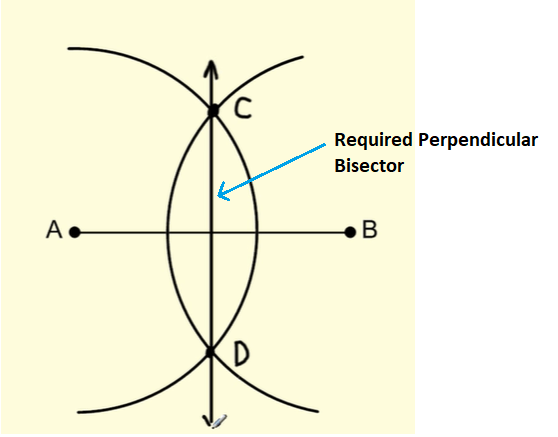
Remarks:
- If we construct the perpendicular bisectors of all three sides of a triangle we obtain the circumcenter of the triangle.
- When constructing a perpendicular bisector why must the compass opening be greater than 1/2 because otherwise the circular arcs drawn using the compass will not meet each other. If we do not obtain intersecting points then we cannot draw the perpendicular bisector.
- Constructing a perpendicular bisector similar to constructing an angle bisector in the sense that in both cases we wish to divide something (a line and an angle respectively) into two equal halves. The word “bisect” literally means dividing something into two equal parts.