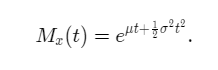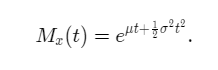Moment Generating Function of Normal Distribution (Step by Step Proof)

In this article, we explain how to derive the moment generating function (MGF) of the normal distribution.

We first calculate the MGF for a standard normal distribution and use a change of variables to find the MGF of the normal distribution.

The MGF of the normal distribution is given by the formula,

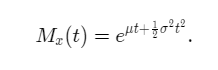
Step 1: Find the Moment Generating Function for Standard Normal Distribution

Let Z be a random variable following the standard normal distribution. The PDF (Probability Distribution Function) of Z is given as,

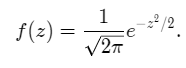
The MGF can be calculated using the formula,

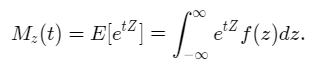
Substituting the PDF in the above expression we get,

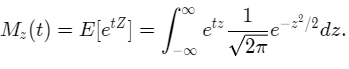
We then collect the terms in the exponent together.

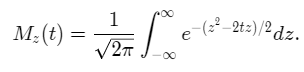
We then complete the square using the formula, (z-t)² = z² – 2zt +t².

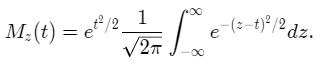
Make the change of variable y = (z-t) to obtain.

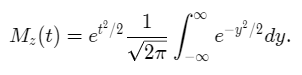
The integrand on the right-hand side above is nothing but the PDF of the standard normal distribution. Since the integral of any probability distribution function is equal to 1, we conclude that

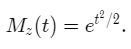
Step 2: Find the MGF for Normal Distribution using a Change of Variable

Let X be a random variable following the normal distribution with mean μ and variance σ². Then Z = (X-μ)/σ follows the standard normal distribution.

We have that X = μ + σ*Z. We can find the MGF of X as follows,

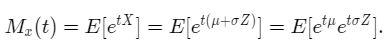
Since e^μt is a constant value not depending on X we can pull it out of the integral sign.

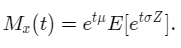
The expectation on the right-hand side above is nothing but the MGF of the standard normal distribution where we substitute tσ instead of t.

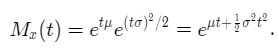
The above expression is the moment generating function of the normal distribution.

Summary

Article Name

Moment Generating Function of Normal Distribution

Description

The MGF of the normal distribution is given by the formula, MGF = exp{μt + σ^2t^2/2}