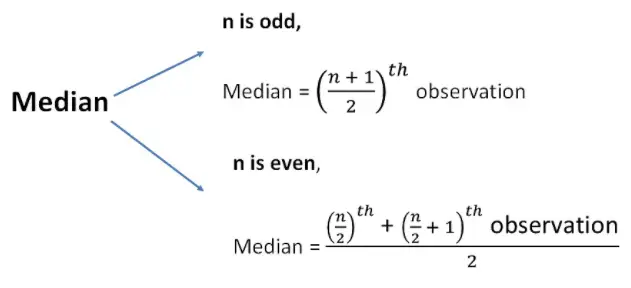
The median refers to the middlemost value in the given data set. There are different formulas for calculating the median depending on whether the number of data values is odd or even.
The Median of Odd Numbers can be calculated using the formula,
Median = [(n+1)/2]th term.
Here, the number of data values ‘n’ is an odd number.
How to find the Median of Odd Numbers:
- We first arrange the data in either ascending or descending order.
- Let n denote the number of data values.
- If n is odd then the median of odd numbers can be found using the formula, Median = [(n+1)/2]th term.
Example 1:
Calculate the median for the following set of data:
3, 9, 7, 6, 5, 2, 8, 11, 9.
Solution: We first arrange the data in ascending order as shown below:
2, 3, 5, 6, 7, 8, 9, 9, 11.
Since we have 9 data values we have that n=9 is odd. Therefore we now use the above formula,
Median = [(n+1)/2]th term.
Median = [(9+1)/2]th term = (10/2)th term.
Median = 5th term = 7.
Example 2:
Calculate the median for the following set of data:
7, 9, 6, 8, 12, 17, 13.
Solution: We first arrange the data in descending order as shown below:
17, 13, 12, 9, 8, 7, 6.
Since we have 7 data values we have that n=7 is odd. Therefore we now use the above formula,
Median = [(n+1)/2]th term.
Median = [(7+1)/2]th term = (8/2)th term.
Median = 4th term = 9.
We can verify that there are three data values lying above 9 and three data values lying below 9. Hence the median divides our data into two equal parts.