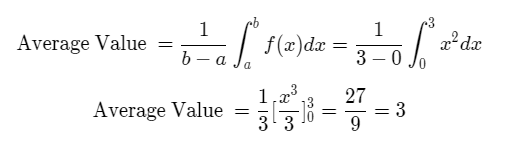Using the concept of integration, we can define the mean or the average value of a function defined on a particular domain.
Suppose that we have a real-valued function f(x) defined on an interval [a,b] then the mean/average value of the function can be calculated using the formula:
Average Value = 1/(b-a) * a∫b f(x)dx.
If f(x) is taken to be a step function with each “step” having the same width then the average value calculated using the above formula coincides with the simple arithmetic mean of the values taken by the function.
Example 1:
Consider the following step function defined on the domain [0,3]:
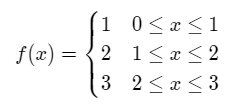
We calculate the mean/average value of the function using the above formula,
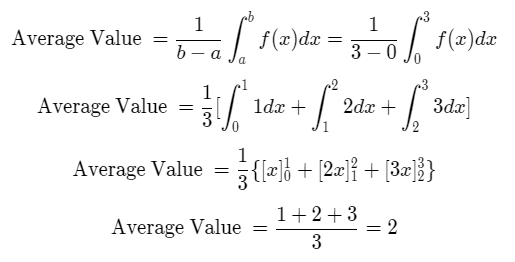
As remarked earlier, the mean value of a step function with each step having equal width has an average value equal to the arithmetic mean of the value taken by the function.
Example 2:
Consider the function f(x) = x2 defined on the domain [0,3]:
We calculate the mean/average value of the function using the formula,