A lurking variable in statistics is a “hidden” variable that we have failed to consider in our model but which has an effect on the response variable. The word “lurking” literally suggests that the variable is unidentified but it still affects our dependent variable.
In observational studies, it is important to identify the presence of lurking variables because they can cause us to misunderstand the relationship between the dependent and the independent variables.
The main reason for the presence of lurking variables is that the researcher fails to identify all the variables that cause changes to occur in the response variable. Let us try to understand what lurking variables are by looking at some examples.
Examples of Lurking Variables:
Example 1: Height and Genetic Factors
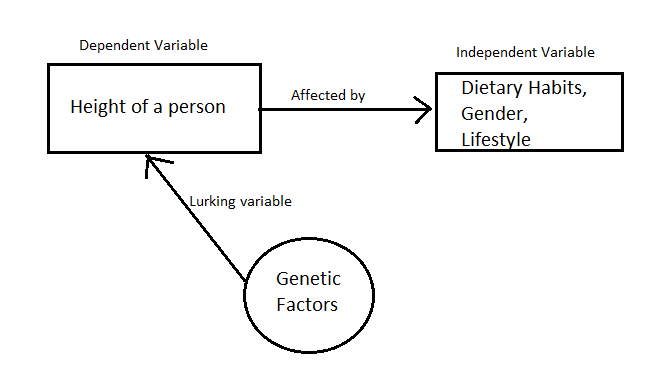
Suppose a researcher develops a statistical model for the height of a person where diet, sex, lifestyle, etc. are taken to be the explanatory variables. It is well known that the height of a person depends on the dietary choices of the person.
Independent Variable: Diet.
Dependent Variable: Height.
In such a case genetic factors may be the lurking variable that the researcher has failed to identify. The researcher has failed to take note of the well known fact that the most important factor that affects the height of the person is the height of the parents.
Lurking Variable: Genetic Factors (Height of Parents).
Example 2: Growth Rate of Crops and Soil Fertility
Suppose that we want to understand the relationship between the growth rate of crops and the amount of fertilizer used. It is to be expected that a higher quantity of fertilizer used would lead to a higher growth rate for crops. Here the amount of fertilizer used is the explanatory variable and the growth rate is the response variable.
Independent Variable: Amount of Fertilizer used.
Dependent Variable: Growth Rate of Crops.
Here the difference in soil fertility among the plots is a potential lurking variable. This is because the growth rate of crops is also affected by the fertility of the soil of the plots.
Lurking Variable: Soil Fertility.
Example 3: Age as a Lurking Variable
It is an empirical fact that the amount of hair that a man has on his head is inversely correlated with the chances of death. This means that a man with less hair on his head is more likely to die.
Does this mean that there is a causal relationship between the two? Does less hair really lead to a man’s death? The answer is clearly no. The reason for this observed relationship is the presence of the lurking variable which is age. The older a man gets the more hair he loses and the greater his chances of death. A 70 year old bald man is much more likely to die than a young 20 year old.
Independent Variable: Hair Loss.
Dependent Variable: Chances of Death.
Lurking Variable: Age.
Example 4: Blood Pressure and Sex
In a linear model for modeling the blood pressure of patients, a researcher takes the explanatory variable to be the diet. The diet of a person has a clear effect on the blood pressure. Here the sex of the patient may turn out to be the lurking variable. This is because it is well known that females generally have a higher heart rate than the male population.
Is Weather a Lurking Variable?
It is well known that there is an inverse correlation between ice cream sales and the sale of sweaters. Does this mean that people who eat ice cream do not buy sweaters? The answer is clearly no.
The lurking variable in this case is the weather. During the summer months, ice cream sales tend to increase, and people do not buy sweaters because of the hot temperature. Conversely, during the winter more people buy sweaters and fewer people eat ice creams because of the cold.
Lurking Variables vs Confounding Variables:
The main difference between the lurking variable and the confounding variable is that the lurking variable is “hidden” and has not been identified by the researcher. On the other hand, the confounding variable also affects the dependent variable but the difference is that the confounding variable has been identified by the researcher who is aware of the effect that it may have on the model.
Both lurking and confounding variables affect the end result of our model even though they are not included in it as explanatory variables. The difference merely lies in whether the researcher is aware of their presence or not.
How to Identify Lurking Variables?
Lurking variables can be identified by the researcher by analyzing the error (residuals) in our model. We can create a residual plot by plotting the residuals on the Y-axis.
If the errors appear to be distributed randomly, obeying the normal distribution then it indicates the absence of a lurking variable. On the other hand, a non-random error pattern indicates the presence of lurking variables.
The researcher may also use his knowledge of the causation involved in the situation. For example, when plotting the residuals to understand the relationship between height and diet the residuals do not appear to be randomly distributed. This is because height acts as a lurking variable.