Indicated probability refers to the probability of a specified event occurring.
For example, suppose that two coins are tossed and we wish to find the probability of getting two heads. We have four possible outcomes {HH, HT, TH, TT} out of which possibility HH is the specified/indicated event. Here the indicated event has a one out of four chance of occurring and therefore,
Indicated probability = ¼ =0.25
So we see that the indicated probability can be calculated by the formula,
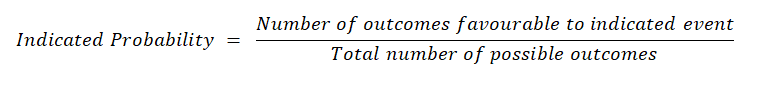
Example 1: Suppose that dice is thrown. Find the probability of getting an even number.
Solution: Here the indicated event is getting an even number. The favourable outcomes are getting 2, 4, and 6 on the face of the dice.
There are a total of 6 outcomes of which 3 are favourable and hence by the above formula,
Indicated Probability = 3/6 = ½ = 0.5
The above example involved calculating dice roll probabilities.
Let us now consider an example of calculating coin toss probabilities.
Example 2: Suppose that two coins are tossed. Find the probability of getting exactly one head.
Solution: Here the indicated event is getting exactly one head. We have four possible outcomes {HH, HT, TH, TT}.
The favourable outcomes are {HT, TH}
There are a total of 4 outcomes of which 2 are favourable and hence by the above formula,
Indicated Probability = Number of favourable outcomes/Number of total outcomes = 2/4 = ½ = 0.5
Additional Rules to calculate indicated probabilities:
- Multiplication rule to calculate probability
- Addition rule to calculate P(A or B) that is, to calculate the probabilities of occurrence of either event A or event B