How to Calculate Grand Mean (with Examples)

The grand mean(also known as combined mean) refers to the average of the entire data when the data has been subdivided into many groups.

Suppose you want to know the average height of students in a school. The students in the school are naturally subdivided according to their grade such as 1^st grade, 2^nd grade, etc.

Using the mean height of students in each grade we can calculate the grand mean, that is, the average height of all the students in the school.

Grand Mean Formula:

The grand mean can be calculated using the formula,

Steps to calculate the Grand Mean:

1. Find out the sample sizes n₁, …, n_k of the subdivisions.
2. Calculate the mean for each of the above subdivisions.
3. Find out the grand mean using the above formula.

Example 1:

Calculate the Grand Mean for the following data subdivided into 2 parts:

[5, 4, 6] [8, 3, 6, 7]

Solution:

Step 1: We note that the sample sizes are n₁=3 and n₂ =4.

Step 2: We calculate the mean for each of the subdivisions as follows,

X̅₁ = 5+4+6/3 = 15/3 = 5.

X̅₂ = 8+3+6+7/4 = 24/4 = 6.

Step 3: Using the formula for grand mean we get,

Grand mean = (n₁*X̅₁ + n₂*X̅₂)/(n₁ + n₂) = (3* 5 + 4* 6)/7 = 39/7 = 5.57.

Example 2:

Calculate the Grand Mean for the following data subdivided into 3 parts:

[1, 3, 2] [7, 4, 5, 8] [7, 5]

Solution:

The sample sizes are n₁=3 and n₂=4 and n₃=2. The mean for each of the subdivisions is,

X̅₁ = 1+2+3/3 = 6/3 = 2.

X̅₂ = 7+4+5+8/4 = 24/4 = 6.

X̅₃ = 7+5/2 = 12/2 = 6.

Grand mean = (n₁*X̅₁ + n₂*X̅₂ + n₃*X̅₃)/(n₁ + n₂ + n₃) = (6+24+12)/9 = 5.

Proof of the Formula for Grand Mean:

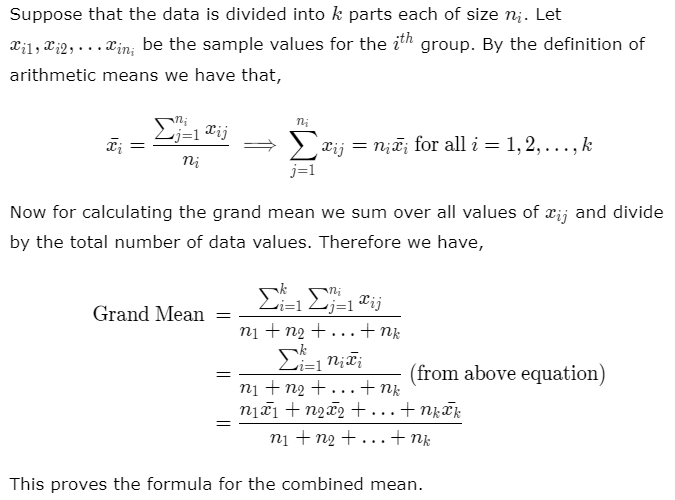
Grand Mean in ANOVA:

The Grand Mean in ANOVA (Analysis of Variance) is used to calculate the total sum of squares TSS.

The TSS is calculated by summing the squares of deviations of all data points from the grand mean and then dividing the result by the total number of data points.