How to Factorise Cubic Equations (with Examples)

A cubic equation refers to any equation containing an x³ term. In order to factorize a cubic equation we must follow the following steps:

Steps to Factorise a Cubic Equation:

1. Let p(x) denote the cubic equation.
2. Try different values to substitute in place of x for which the resulting value is 0. Suppose you find an ‘a’ such that p(a)=0.
3. By the factor theorem, we can conclude that (x-a) is a factor of p(x).
4. Perform long division to divide p(x) by (x-a). Let q(x) denote the quotient.
5. We have that p(x) = (x-a)q(x). Now the quotient q(x) is a quadratic which can be factorized using the usual method of splitting the middle term.

Example 1: Factorise the cubic polynomial p(x) = x³ – 2x² – 9x + 18.

Solution: We try various values of x. For example, x=1 gives p(1)=8 which is nonzero and therefore does not work.

Let us now try x=2. We have that p(2)=2³ – 2(2)² – 9(2) + 18 = 0.

So the required value for ‘a’ is 2 and we conclude that x-2 is a factor of p(x). We now perform long division as shown below.

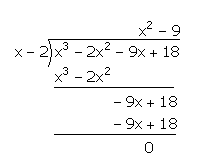
p(x)=x³ – 2x² – 9x + 18 = (x-2)(x²-9).

x³ – 2x² – 9x + 18 = (x-2)(x²-3²).

x³ – 2x² – 9x + 18 = (x-2)(x-3)(x+3).

Example 2: Factorise the cubic polynomial p(x) =  2x³ + 5x^2 – 28x – 15.

Solution: As a guess, we substitute x=-5 in the above cubic equation. We have that p(-5)=2(-5)³ + 5(-5)² – 28(-5) – 15 = 0.

So the required value for ‘a’ is -5 and we conclude that x+5 is a factor of p(x). We now perform long division as shown below.

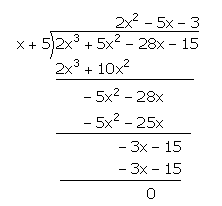
p(x)=2x³ + 5x² – 28x – 15 = (x + 5) (2x² – 5x – 3).

2x³ + 5x² – 28x – 15= (x + 5) (2x² – 6x + x – 3).

2x³ + 5x² – 28x – 15= (x + 5) [2x(x – 3) + 1(x – 3)].

2x³ + 5x² – 28x – 15 = (x + 5) (2x + 1) (x – 3).