The expected value of x3 can be calculated using the formula,
E(X3) = Σ x3 * p(x)
- Here p(x) is the probability mass function for the discrete random variable X.
- The sum Σ x3p(x) is taken over all values of Xi from i=1 to n.
In this article, we will explain how to calculate the expected value of X3 where X can be any continuous or discrete random variable.
For a discrete random variable, the expected value is calculated by multiplying the cube of the random variable by the pdf and summing up all possible values of x.
For a continuous random variable, it is found by integrating the x3f(x) over the domain of f(x). Here f(x) is the probability distribution function of X.
Example 1:
Consider a discrete random variable X whose probability mass function is given as follows,
| X | Probability P(X) |
| -2 | 0.1 |
| -1 | 0.2 |
| 0 | 0.3 |
| 1 | 0.3 |
| 2 | 0.1 |
In order to calculate the required value, we first create columns to calculate the values of x3 and x3p(x).
| X | P(X) | X3 | X3*P(x) |
| -2 | 0.1 | -8 | -0.8 |
| -1 | 0.2 | -1 | -0.2 |
| 0 | 0.3 | 0 | 0 |
| 1 | 0.3 | 1 | 0.3 |
| 2 | 0.1 | 8 | 0.8 |
We now sum up the values of the last column as required by the formula,
E(X3) = Σ x3 * p(x) = (-0.8) + (-0.2) + 0 + 0.3 + 0.8 = 0.1
Example 2 – Continuous Random Variable:
Let X be a continuous random variable with probability distribution function f(x). Then the required expected value can be calculated using the formula,
E(X3) = ∫ X3 f(x) dx
Illustration:
Let X be a continuous random variable with the pdf of X given as follows,
f(x) = 2x where, 0 < x < 1
We now calculate the expected value of x3 as follows,
E(X3) = ∫ X3 f(x) dx
E(X3) = 0∫1 2x4 dx = [2x5/5]01 = 2/5 = 0.4.
Thus the required expected value is 0.4.
Does the expected value of x3 equal mu_3?
The expected value of X3 refers to the third raw moment of the random variable whereas the symbol µ3 (mu_3) refers to the third central moment of the random variable. Thus we conclude that these two quantities are not equal to each other.
The third raw moment is denoted by the symbol µ3‘ (mu_3 prime). Thus we conclude that the expected value of X^3 is equal to µ3‘.
Ways to get the Expected Value of X^3:
One way to get the expected value is to use the formula above and obtain the expected value by integrating the value of x3f(x) over the possible values of X.
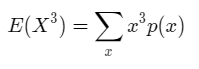
Another way to calculate the required expected value is by using the moment-generating function of the random variable. If we differentiate the moment-generating function three times and then put t=0 we obtain the required expected value.
Related Articles:
- How to find the Expected Value of X^2 (with Examples).
- Expected value of the product of random variables.
- Central Moments and Raw Moments in Statistics.