The Exogeneity assumption is one of the assumptions in a linear regression model. It means that the dependent variable does not causally affect the independent variables.
The independent and dependent variables are correlated but the causal link is only in one direction – the independent variable affects the dependent variable not vice-versa.
If the assumption of exogeneity is not satisfied then the estimates obtained using the model may not be accurate.
Example of a situation where the Exogeneity assumption is violated:
Suppose we construct a linear regression to model the effect of agricultural growth (independent variable X) on the income of a farmer (dependent variable Y). Obviously, if there is more agricultural growth then the income of the farmer increases.
But if the income of the farmer increases, the wealth is further invested into the farm, and the agricultural growth of the farm increases. Here we see that the dependent variable is affecting the independent variable and the assumption of exogeneity is being violated.
Example of a situation where the Exogeneity assumption is obeyed:
Suppose we construct a linear regression to model the effect of rainfall (independent variable X) on the yield of wheat grown in a farm (dependent variable Y). Rainfall is necessary if we want the crops to grow so the independent variable is affecting the dependent variable. But the growth of crops cannot cause rainfall so the causal link is in one direction only.
How to check for exogeneity?
We can use Hausman’s test to check whether the exogeneity assumption is satisfied. We can easily carry out the test for checking endogeneity in Stata software.
Formal Mathematical Definition of Exogeneity Assumption:
The formal definition for exogeneity is that,
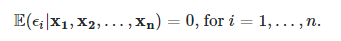
where, ε is the error term.
It means that the error has mean 0 and is not correlated with the independent variables.