It is indeed possible for a matrix to have an eigenvalue that is equal to zero. If a square matrix has an eigenvalue of zero, then it means that the matrix is singular (not invertible).
Recall that we say that a matrix A has eigenvalue λ, if there exists a nonzero vector v such that,
Av = λv.
In particular, the vector v≠0 is called an eigenvector for the matrix.
Note that it is by definition impossible for an eigenvector to be zero. On the other hand, it is possible that the eigenvalue is zero.
If an eigenvalue of A is zero, it means that the kernel (nullspace) of the matrix is nonzero. This means that the matrix has a determinant equal to zero. Such a matrix will not be invertible.
The converse of the above statement is also true. If a matrix A has determinant equal to 0, it means that 0 is an eigenvalue for the matrix. We now give an example of a matrix that has a zero eigenvalue.
Example:
Consider the matrix,
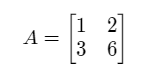
The characteristic polynomial of the matrix is given as,
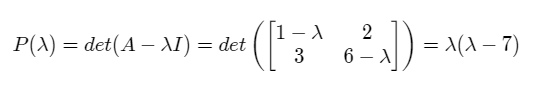
Solving P(λ) = 0 we see that, the matrix A has eigenvalues 7 and 0. Notice that matrix A is not invertible (since it has determinant equal to 0).