The counting rules are used in combinatorics and probability to calculate the number of ways in which we can get a certain outcome. The two most common rules are the multiplication rule and the addition rule.
Multiplication Counting Rule:
The multiplication counting rule says that if there are ‘m’ number of outcomes of a certain event followed by ‘n’ number of ways of outcomes for another event, then the total number of outcomes when the events occur one after another is ‘m*n’.
So it simply means that we should multiply the individual number of outcomes to find the total number of outcomes in which two events can occur one after the other.
Example 1: Suppose that there are three bridges between city A and city B and there are 2 bridges between city B and city C. In how many ways can you reach from city A to city C?
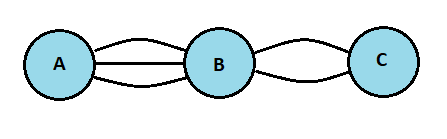
Solution: Since there are 3 ways of going from city A to B followed by two ways of going from city B to city C by using the multiplication rule we conclude that,
Number of ways of going from city A to C = 3*2 = 6
Example 2: Suppose that a person has 3 shirts, 5 trousers, and 4 different kinds of socks. In how many ways can the person choose an outfit to wear?
Solution: Since there are 3 possibilities for choosing a shirt followed by 5 possibilities for trousers and 4 possibilities for choosing socks by using the multiplication rule we conclude that,
Number of possible outfits = 3*5*4 = 60
Example 3: How many four-letter words (with or without meaning) can be formed by using the alphabets of the English language? The letters are used without repetition.
Solution: There are 26 possibilities for the first letter of the word.
Since one of the letters has been used there are remaining 25 possibilities for the second letter of the word.
Similarly, there are 24 and 23 possibilities for the third and fourth letters of the word.
By using the multiplication rule we get,
Number of possible four-letter words = 26*25*24*23 = 358800
Addition Counting Rule:
The addition counting rule says that if there are two mutually exclusive events A and B then the number of ways in which A or B can occur is equal to the sum of the number of ways in which the individual events can occur.
This means that we simply add the number of possible outcomes in which A and B.
Example: If the cities A, B, and C are connected by bridges as shown in the below image, then find the number of ways in which we can get from city A to city C.
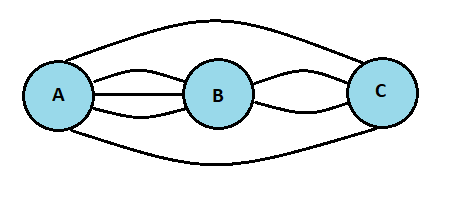
Solution: Case 1: If we travel via the upper bridge then there is only 1 possible way to go from city A to B.
Case 2: If we travel via the lower bridge then there is once again only 1 possible way to go from city A to B.
Case 3: If we travel via the bridges in the middle then by the multiplication rule explained above there are 3*2=6 possible ways to go from city A to B.
Since the above three cases are mutually exclusive by the addition rule we conclude,
Number of ways from city A to city C = 1+1+6 = 8 possible ways.