The value of cos(π/4) is equal to cos(45) = 1/√2 = √2/2. In decimal form, this value is cos 45 degrees is approximately equal to 0.707.
Why is cos(pi/4)= 1/√2 ?
Recall that π (“pi”) radians are equal to 180 degrees. Therefore, pi/4 radians are equal to 180/4 = 45 degrees. We want to find the values of cosine 45 degrees. For this, we can use the definition of cos.
The ratio cos is defined as the ratio of the adjacent side to the hypotenuse in a right-angled triangle. Consider the right-angled triangle ABC as shown below:
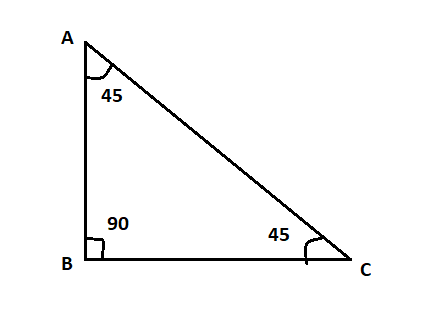
In the above image, the triangle is right-angled at vertex B. Both angles A and C is equal to 45 degrees each.
This means that the above triangle is an isosceles triangle meaning that the two sides AB and BC are equal. Let us denote the two sides as x.
We now apply the Pythagoras theorem which tells us that,
AC2 = AB2 + BC2.
AC2 = x2 + x2.
AC2 = 2x2 that is, AC=x√2.
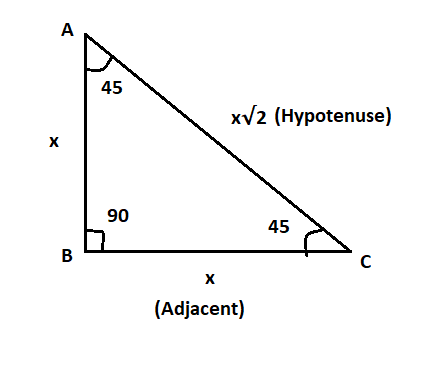
We now use the definition of the cosine of an angle. Notice that side BC is adjacent to angle C and that AC is the hypotenuse of our triangle. We have that,
cos(C) = cos(45) = Adjacent/Hypotenuse = BC/AC = x/x√2 = 1/√2.