The commutative property of multiplication means that the order in which two numbers are multiplied does not matter. For instance, 4 x7 = 28 and 7×24 =28. So the order in which 7 and 4 are multiplied does not matter since the end result(=28) is the same in both cases.
This property can be remembered by the fact that the word “commute” in English means moving/traveling. The two numbers can “travel” and exchange places with each other without having any effect on the final answer.
Why is the Commutative Property of Multiplication true?
Let us try to understand why the commutative property is true by looking at the following example. In the below image, we have some red balls arranged in a rectangular shape. Clearly, if we want to count the total number of balls it does not matter if we count the rows first or if we count the columns first.
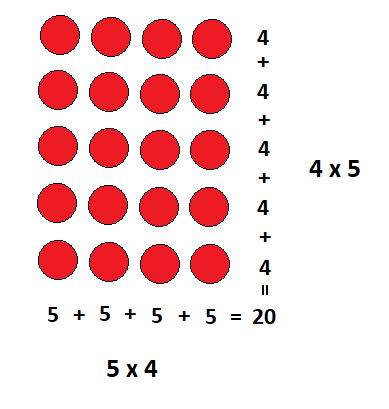
Suppose that we count the red balls by rows. We have four balls in the first row, followed by four in the second, and so on. Counting the balls row-wise in this way we have that,
Number of Balls = 4 + 4 + 4 + 4 + 4 = 20.
But adding 4 to itself 5 times is the same as multiplying 4 by 5. Therefore,
Number of Balls = 4 x 5.
Similarly, we have 5 balls in each column and so if we count the balls in a column-wise fashion we have that,
Number of Balls = 5 + 5 + 5 + 5 = 20.
Once again since adding 5 to itself 4 times is nothing but multiplying 5 by 4 so we have that,
Number of Balls = 5 x 4.
Since the total number of balls remains the same and does not depend on the manner of counting we see that multiplication must be commutative. In our example above we multiplied two integers 4 and 5.
But the commutative property holds in general for all real numbers (fractions, decimal numbers, rational numbers, irrational numbers).
The argument seen above gives a kind of “proof” for the commutative property of multiplication. Given any two integers, we can draw a corresponding rectangle for the two numbers and use it to conclude that the order of multiplication is irrelevant.
Formal Statement of Commutative Property:
Let a and b be two real numbers. Then we can multiply the two numbers in any order, that is, for any two real numbers a and b
a x b = b x a.
It is important that we explicitly state that the commutative property holds for the multiplication of real numbers. This is because “numbers” are not the only object that one deals with in mathematics.
In higher mathematics there exist objects such as “matrices” and “vectors” for which multiplication may not be commutative.