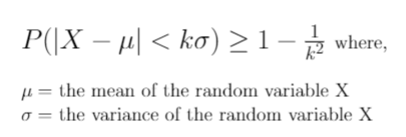Chebyshev’s inequality is an inequality that tells us the probability of a random variable lying a certain number of standard deviations away from the mean.
This theorem was discovered by the Russian mathematician Chebyshev in 1853 and later rediscovered by Bienayme.
Chebyshevs Formula:
The formal mathematical form of Chebyshev’s inequality is,
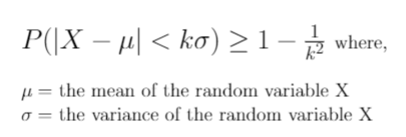
The inequality can also be alternatively stated in the opposite form as,
P(|X-μ|>kσ) ≤ 1/k2.
Examples of Chebyshev’s Inequality:
1. If we put k=3 in the first inequality above then we get,
P(|X-μ|<3σ) ≥ 1-(1/9) that is,
P(|X-μ|<3σ) ≥ 0.89.
This means that 89% of the data values in a distribution lie within 3 standard deviations away from the mean.
2. Similarly if we put k=2 in the above inequality we get,
P(|X-μ|<2σ) ≥ 1-(1/4) that is,
P(|X-μ|<2σ) ≥ 0.75.
This means that 75% of the data values in a distribution lie within 2 standard deviations away from the mean.
Uses of Chebyshev’s Formula:
- Chebyshev’s inequality can be used to obtain upper bounds on the variance of a random variable.
- The Chebyshev inequality can also be used to prove the weak law of large numbers.
- The weak law of large numbers tells us that if we draw samples of increasing size from a population then the sample mean tends toward the population mean.
- As seen above the Chebyshev Formula gives us results similar to the empirical rule.
- It tells us what percentage of the data lies within a certain distance from the mean.
- The difference is that the empirical rule is only applicable to normal distributions whereas the Chebyshev formula is applicable to every distribution.
- Since the empirical rule applies only to a specific case it is much more sharper and accurate when compared to the Chebyshev inequality.
Chebyshev Inequality Proof:
The Chebyshev inequality can be proved by elementary probabilistic arguments as shown below. We first assume that the variable is a continuous random variable. We begin with the definition of the variance of a random variable.
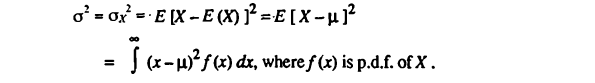

If the random variable is discrete then the Chebyshev inequality follows in the same way as above except for the fact that integration is replaced by summation everywhere in the above proof.
One-Sided Chebyshev Inequality:
Suppose now that we are interested in the fraction of data values that exceed the sample mean by at least k sample standard deviations.
We assume that k is a positive integer. In this case, we use the one-sided Chebyshev inequality which states that
P(X-μ>kσ) ≤ 1/(1+k2).
Notice that this is different from the usual Chebyshev inequality because the usual Chebyshev inequality tells us the fraction of data values to the left and right of the sample mean that differ from it by at least k sample standard deviations.
The one-sided inequality gives us only those fraction of values that are to the right of the sample mean and that differ from it by at least k sample standard deviations.