Difference between binompdf and binomcdf

The binompdf and binomcdf are two commands in a TI calculator that can be used to calculate probabilities associated with the binomial distribution.

A binomial distribution has two parameters ‘n’ which is the number of trials and ‘p’ which is the probability of success in a particular trial.

1. The function binompdf(n, p, x) accepts the value of the n and p and tells you the probability that there are exactly x number of successes in ‘n’ trials. This basically means that this function outputs the probability mass function of the binomial random variable.
2. The function binomcdf(n, p, x) accepts the value of the n and p and tells you the probability that there are less than or equal to x number of successes in ‘n’ trials. This basically means that this function outputs the cumulative distribution function of the binomial random variable.

Example of binompdf command:

Suppose that an archer tries to hit a target 7 times. It is known that the archer succeeds in hitting the target 35% of the time. Calculate the probability that the archer hits exactly 4 targets out of 7.

Solution:  We are given n=7 and p=probability of success = 35% = 0.35

We want to find the probability of exactly 4 successes therefore we use the command binompdf(7,0.35,4).

Click on 2^nd on the TI calculator and then click on DISTR which gives displays a list of distributions. Scroll down to reach the binompdf() command.

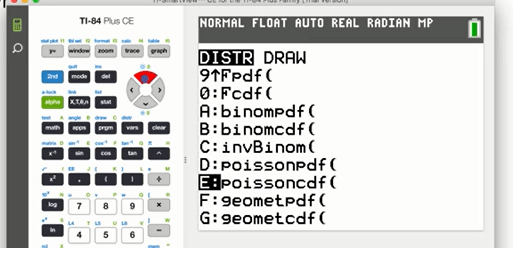
Input the values of n, p, and x given above and press enter. We get an output that looks like

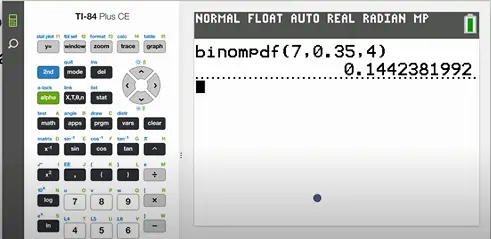
Therefore we conclude that there is a 14.42% chance that the archer hits exactly 4 targets out of 7.

Example of binomcdf command:

Suppose that an archer tries to hit a target 7 times. It is known that the archer succeeds in hitting the target 35% of the time. Calculate the probability that the archer hits less than or equal to 4 targets out of 7.

Solution:  We are given n=7 and p=probability of success = 35% = 0.35

We want to find the probability of less than or exactly 4 successes therefore we use the command binomcdf(7,0.35,4).

We click on 2^nd on the TI calculator and then click on DISTR and scroll down to reach the binomcdf() command.

We input the values of n, p, and x given above and press enter. We get an output that looks like

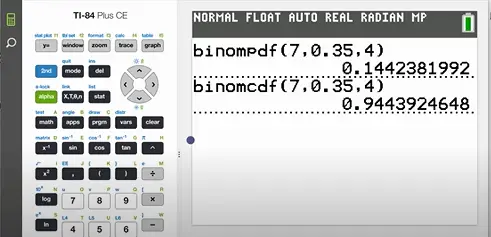
Therefore we conclude that there is a 94.43% chance that the archer hits less than or equal to 4 targets out of 7.